Notes
a square and a triangle solution
Solution to the A Square and a Triangle Puzzle
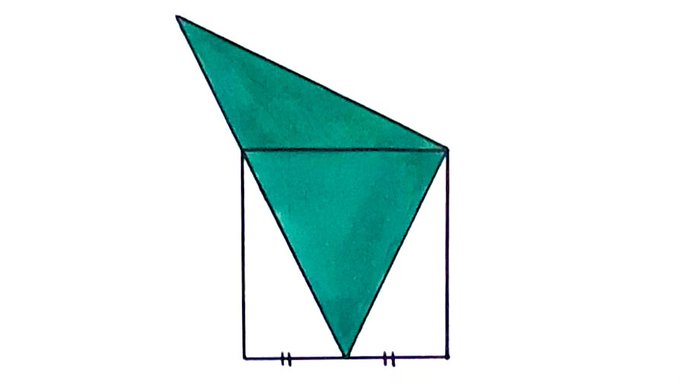
The square has area 36. What’s the area of the right-angled triangle?
Solution by Similar Triangles
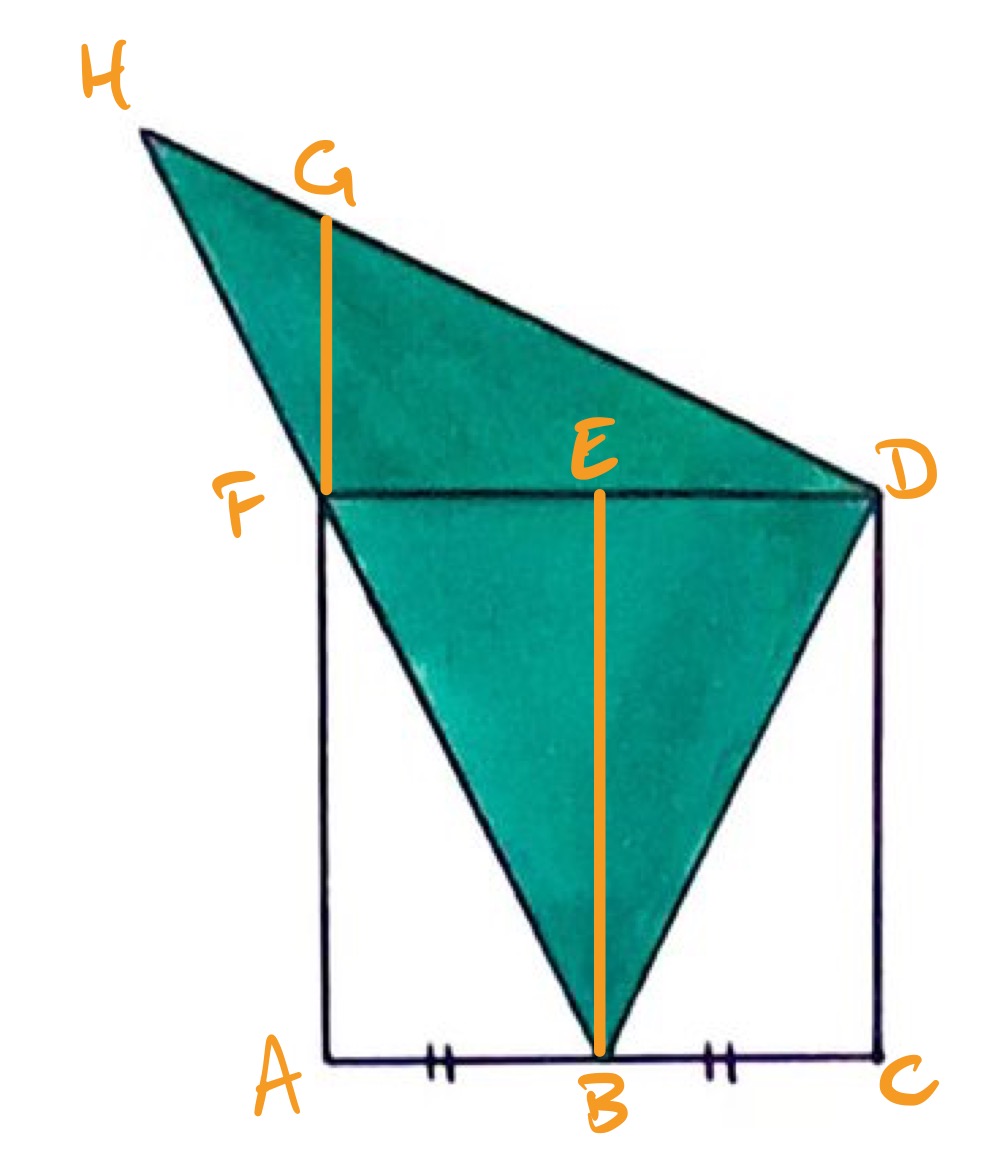
In the diagram above, is the midpoint of and is such that angle is a right-angle. Triangle has area one quarter that of the square, which is .
Since angle is a right-angle, angles and add up to . Since triangle is also right-angled, so also angles and add up to . Therefore, angles and are equal. Then and are the same length, so triangles and are congruent.
Angles and add up to , since together with , which is a right-angle, they are angles at a point on a straight line. So angle is the same as . This means that triangles and have the same angles (they also both share ) and so are similar. The edges and correspond, and since has the same length as , this means that the length scale factor from to is . The area scale factor is therefore .
Hence triangle has four times the area of triangle . This means that triangle has three times the area of triangle . Since has area , this means that triangle has area .
The total shaded area is then .
Solution by the Double Angle Formula of Trigonometry and Pythagoras' Theorem
Let be angle . Since the area of the square is , its side length is and so then has length . Therefore, .
Angle is and so by the double angle formula its tangent is given by:
Using Pythagoras' theorem, the length of is:
So then the length of is . The area of the shaded triangle is then: