Notes
a square and a rectangle overlapping solution
A Square and a Rectangle Overlapping
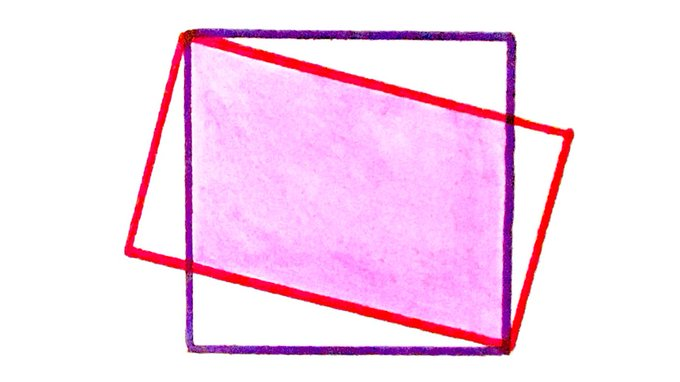
of the purple square is shaded. What percentage of the red rectangle is shaded?
Solution by Pythagoras' Theorem and Area of a Triangle and Rectangles
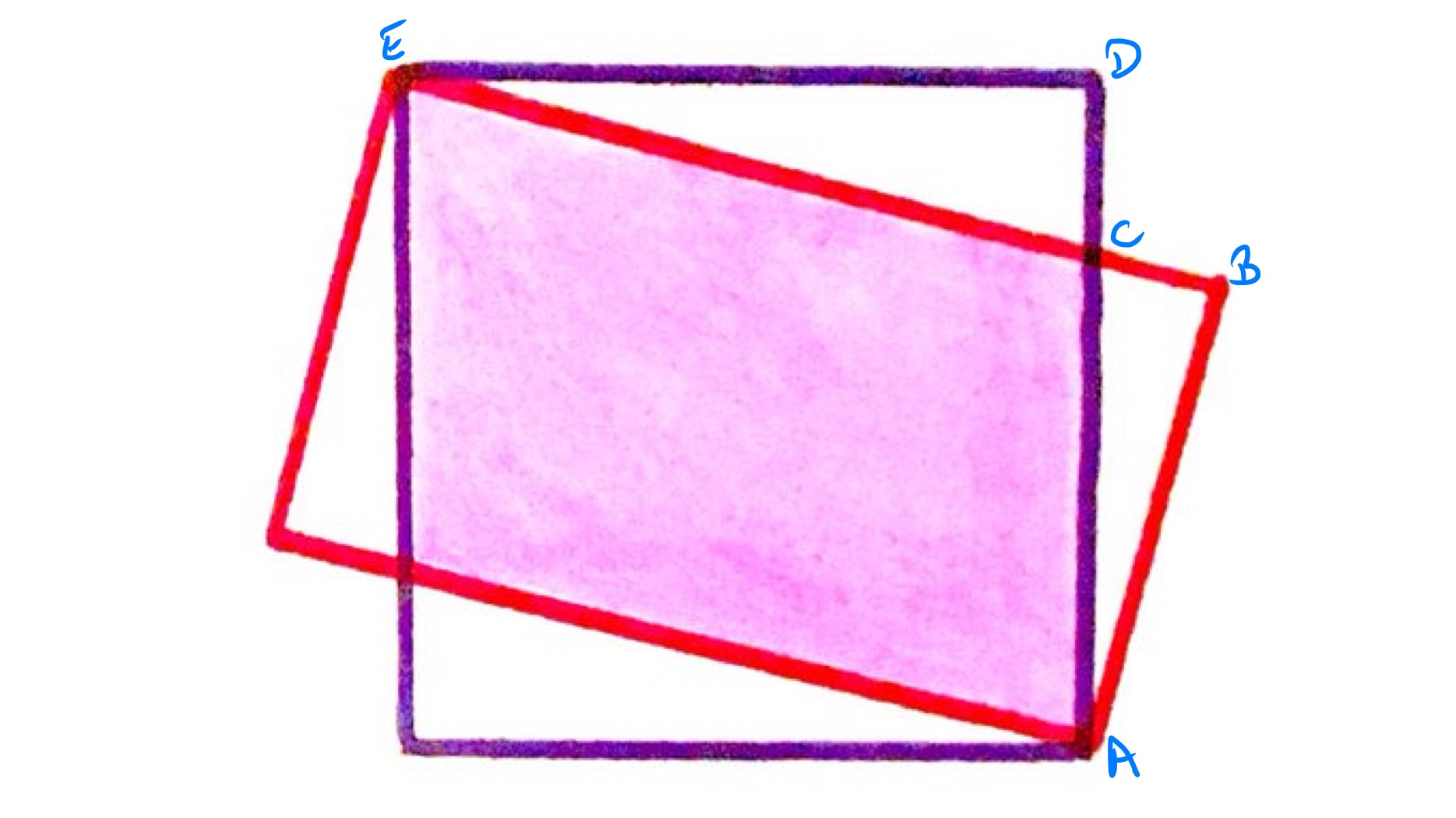
With the points labelled as above, the fact that of the purple square is shaded means that the length of is one quarter of the length of . Since the purple quadrilateral is a square, is the same length as . Let be the length of , so has length . Applying Pythagoras' theorem to triangle shows that the length of is . The ratios of the sides of triangle is therefore .
Triangles and are both right-angled triangles and angles and are equal as they are vertically opposite so triangles and are similar. As the length of is , the lengths of triangle are , , and . The length of is therefore .
The ratio of the lengths of and is therefore and so the percentage of the red rectangle that is shaded is .