Notes
a square, triangle, and circle in a square solution
A Square, Triangle, and Circle in a Square
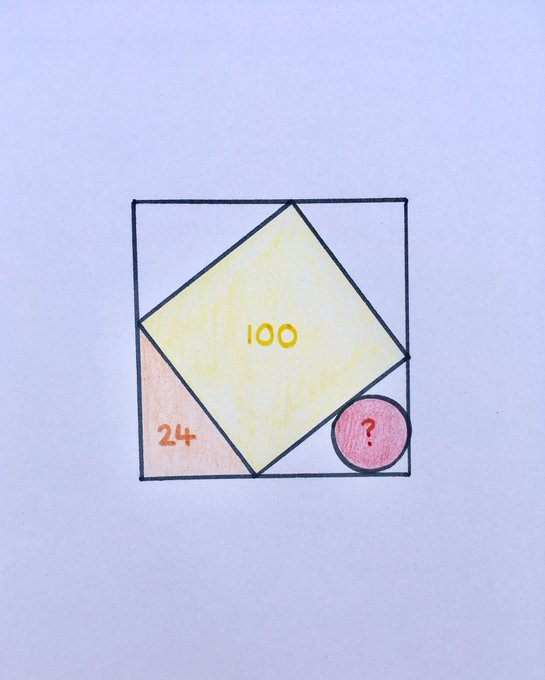
The square, circle and triangle are stacked inside a larger square. What’s the area of the circle?
Solution by Pythagoras' Theorem
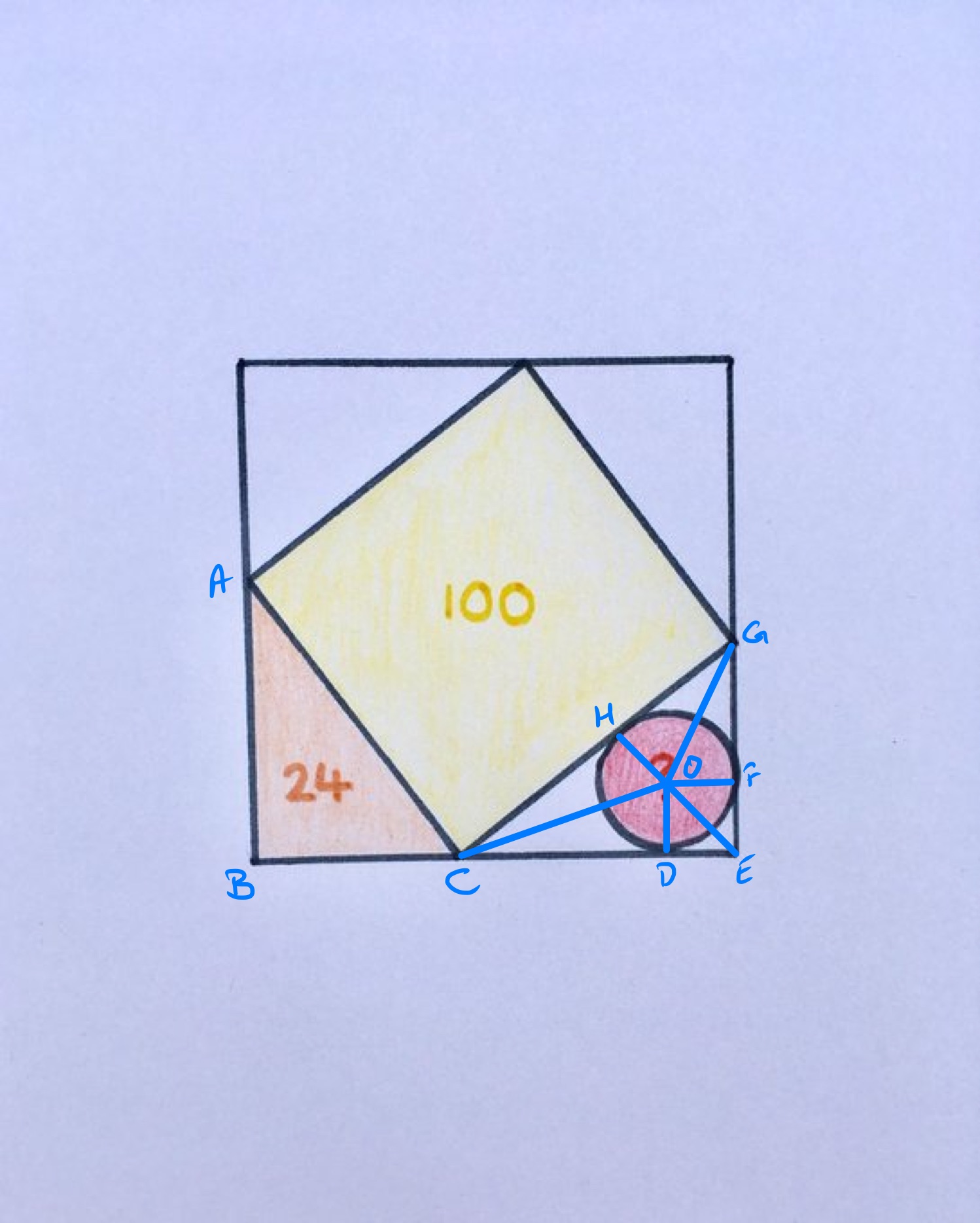
Let , , be the lengths of the sides of triangle , so that has length , of length , and of length . Since the central square has area , . The area of the triangle is given by so . Applying Pythagoras' theorem to this triangle shows that . Putting these together, , so .
Triangle is congruent to triangle . Inside that triangle, and have the same length, as to and . So the combined lengths of and give the difference between the combination of and and the length of . So has length and so the area of the circle is .