Notes
a square, a circle, and a rectangle solution

A Square, A Circle, and a Rectangle

Solution by Pythagoras' Theorem and Lengths in Circles

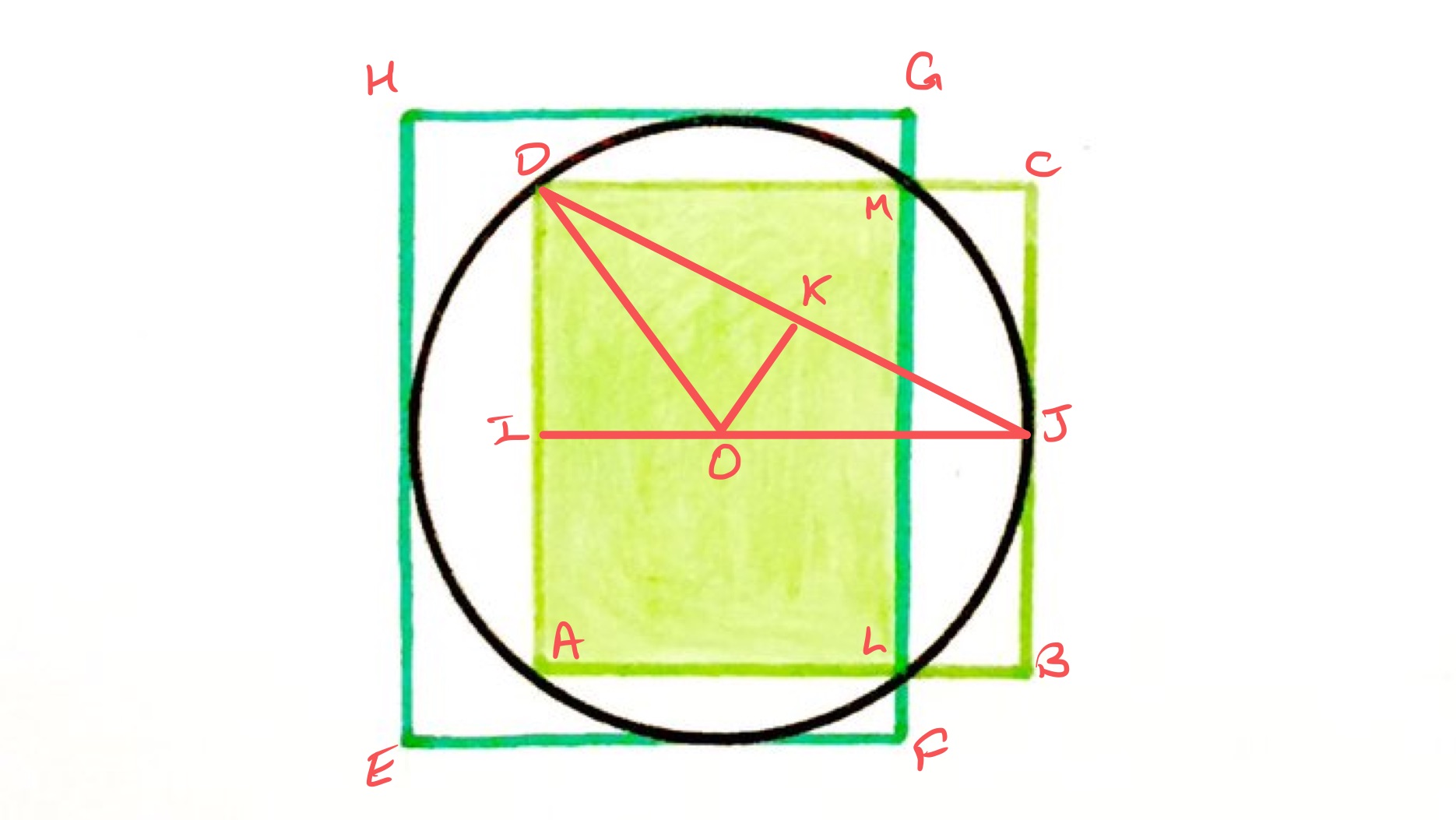
In the above diagram, the point labelled $O$ is the centre of the circle and the point labelled $K$ is the midpoint of the line segment $D J$.

Let $x$ be half the length of the side of the square, so that $I D$ has length $x$. Then triangle $D I J$ is a right-angled triangle with short sides of lengths $x$ and $2 x$. Using Pythagoras' theorem, its hypotenuse is then $\sqrt{5} x$.

Since $O J$ and $O D$ are both radii of the circle they are the same length. Therefore triangle $D O J$ is isosceles and so the line segment $O K$ splits it into two equal right-angled triangles. As triangle $O K J$ shares an angle with triangle $D I J$ at $J$, they are similar. The length of $J K$ is $\frac{\sqrt{5}}{2} x$ so the length scale factor is $\frac{\sqrt{5}}{4}$. The length of $O J$ is therefore $\frac{\sqrt{5}}{4} \times \sqrt{5} x = \frac{5}{4} x$.

Since $I J$ has length $2 x$, $O I$ must therefore have length $\frac{3}{4} x$ which means that $D M$ has length $\frac{3}{2} x$. So the shaded area is a rectangle of dimensions $\frac{3}{2} x$ and $2 x$ so has area $3 x^2$. The outer rectangle has width $2 x$ and height $2 \times \frac{5}{4} x = \frac{5}{2}x$ so has area $5 x^2$. Finally, the square has area $4 x^2$.

The total area of the shape is therefore $4 x^2 + 5 x^2 - 3 x^2 = 6 x^2$ and so half of the full shape is shaded.