Notes
a semi-circle and a quarter circle in a rectangle solution
Solution to the A Semi-Circle and a Quarter Circle in a Rectangle Puzzle
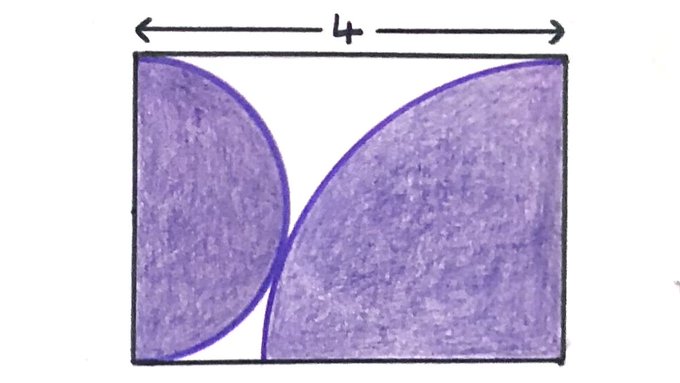
What’s the shaded area?
Solution by Pythagoras' Theorem and the Area of a Circle
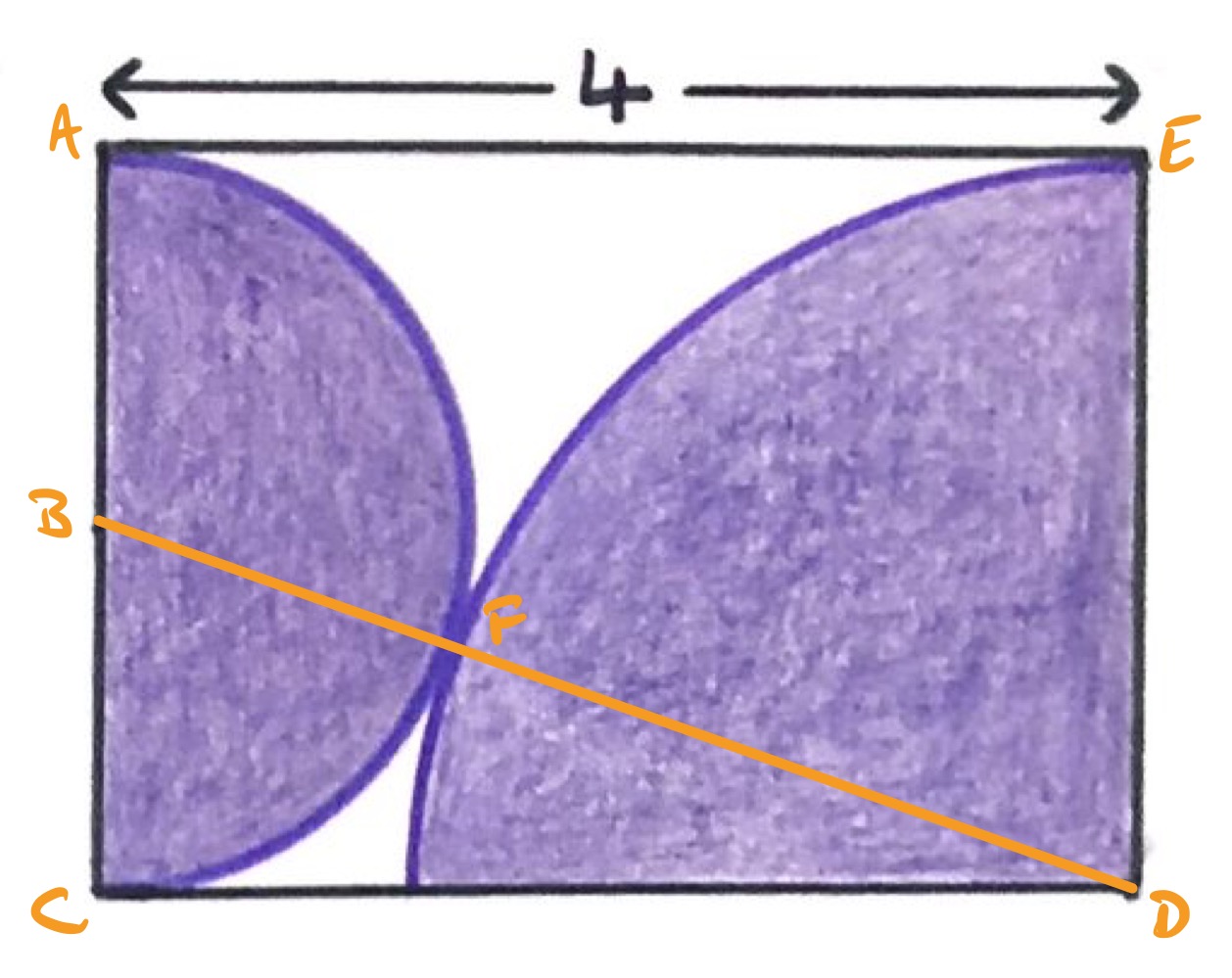
Label the points as above, where is the centre of the semi-circle and is the point where the circles meet. Then is a straight line.
Let be the radius of the semi-circle, so the vertical side of the rectangle has length , and this is then the radius of the quarter circle. In terms of , the shaded area is:
Triangle is right-angled, so it satisfies Pythagoras' theorem. Its side lengths are , , and , so:
so and hence .
The shaded area is therefore .