Notes
a rectangle in a square solution
Solution to the Rectangle in a Square Puzzle
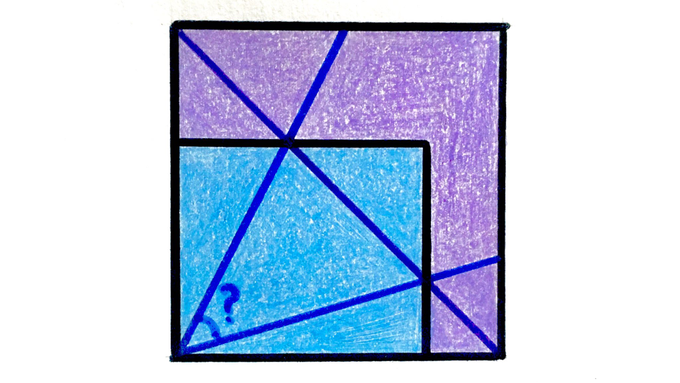
The blue rectangle covers half of the square’s area. What’s the angle?
Solution by Angle at the Centre is Twice the Angle at the Circumference and Pythagoras' Theorem
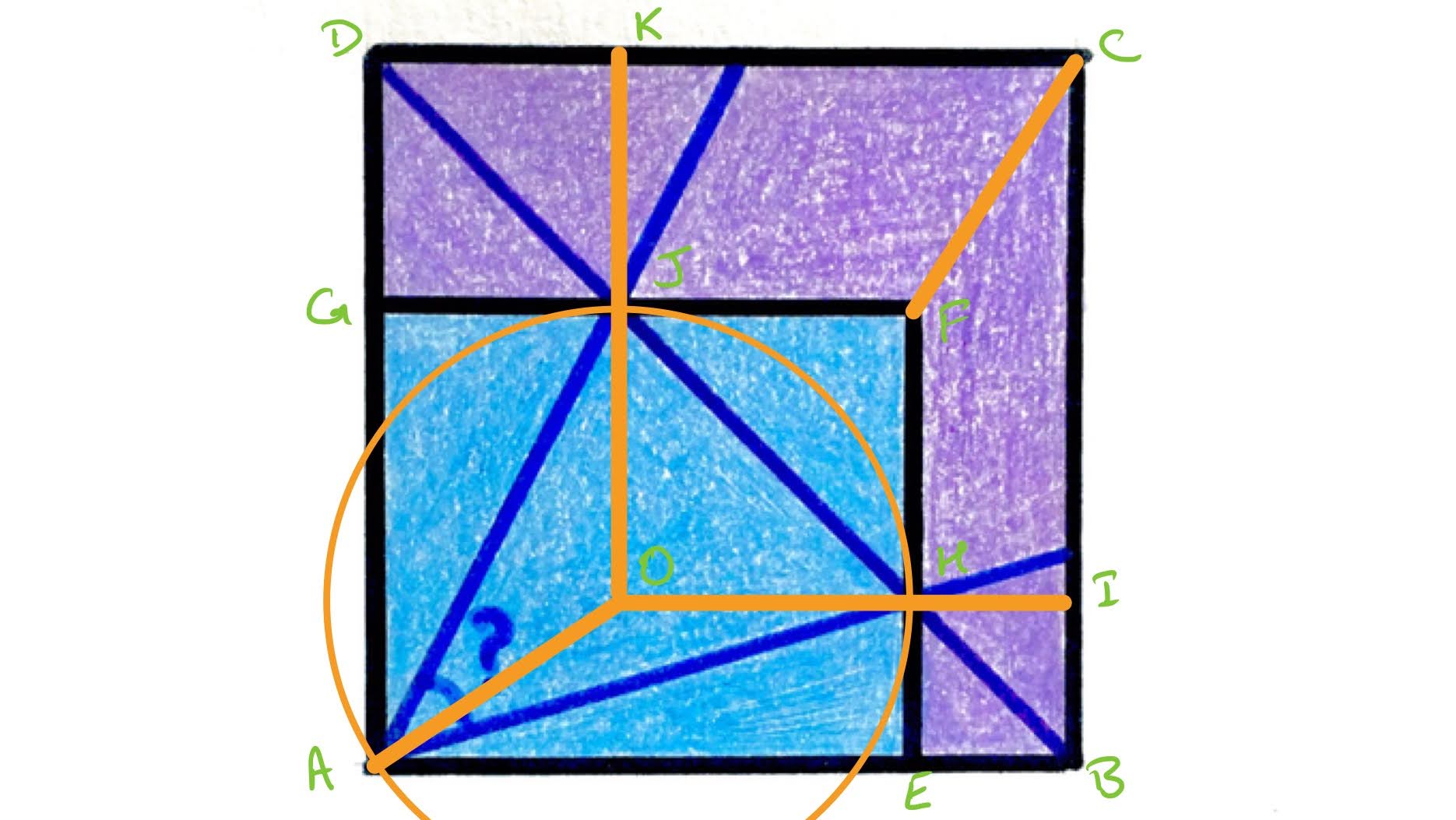
In the above diagram, the line segment is vertical and passes through , while is horizontal and passes through . The line segment is at to the horizontal and vertical, so the line segments and have the same length and this establishes as a square. The circle has centre and passes through , then since and have the same length, it also passes through .
To see that it also passes through , consider the line segment . Using Pythagoras' theorem, the square of the length of is the same as the sum of the squares of the lengths of and .
The blue rectangle occupies half of the area of the square. By reflecting in the line , it can be seen that the region matches . Therefore, the central square must have the same area as the two squares and . This means that the squares of the lengths of and is equal to the square of the length of , and hence has the same length as . Therefore lies on the circle.
The angle is a right-angle, and is the centre of the circle, so by the result that the angle at the centre is twice the angle at the circumference, angle is .
Solution by Invariance Principle
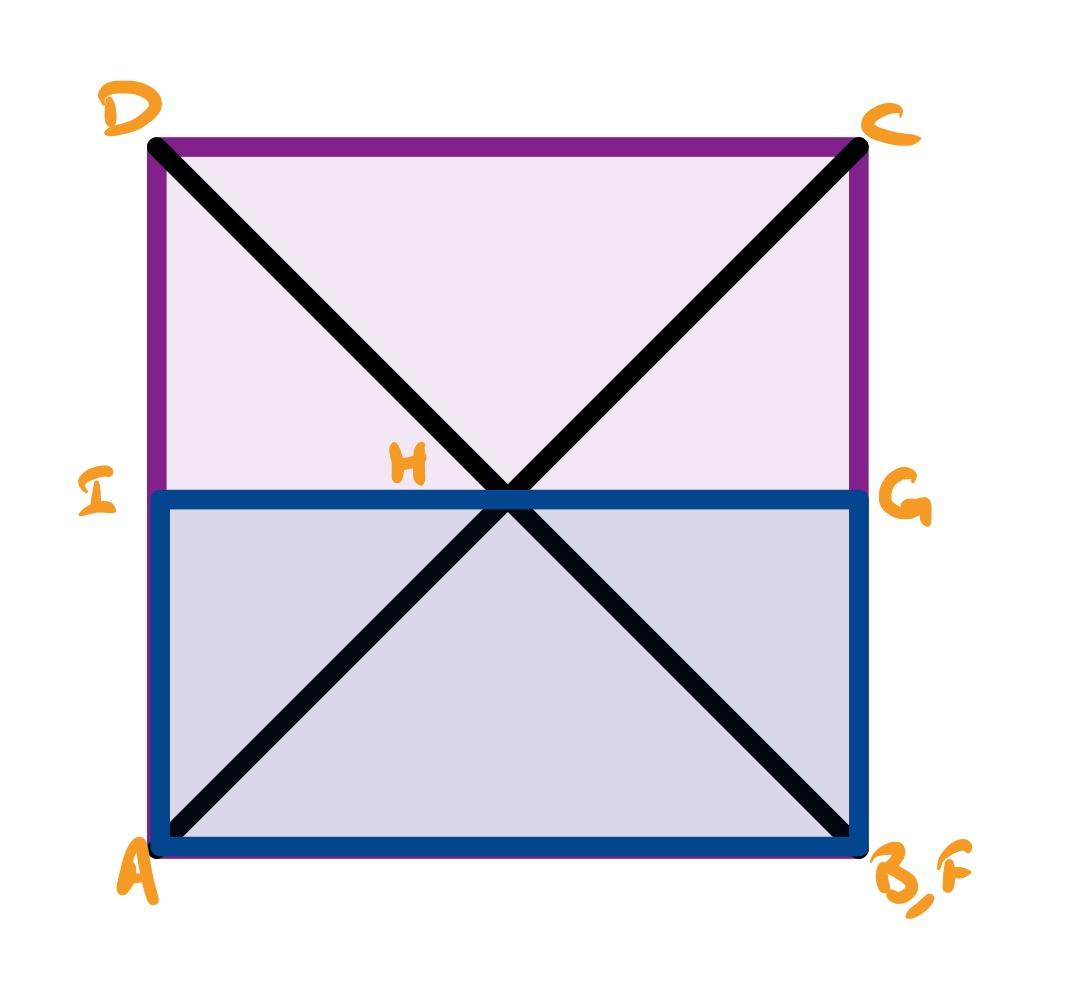
The point can move providing the area of the rectangle remains half of the area of the square. It can therefore move so that it lies on the edge , at which point it must be the midpoint of that edge. The point then coincides with (and ) and the intersection of with the edge is its midpoint, which is the centre of the square. The line is therefore the other diagonal and so angle is .