Notes
a pattern of squares solution

Solution to the A Pattern of Squares Puzzle

Solution by Area of a Square and Dissection

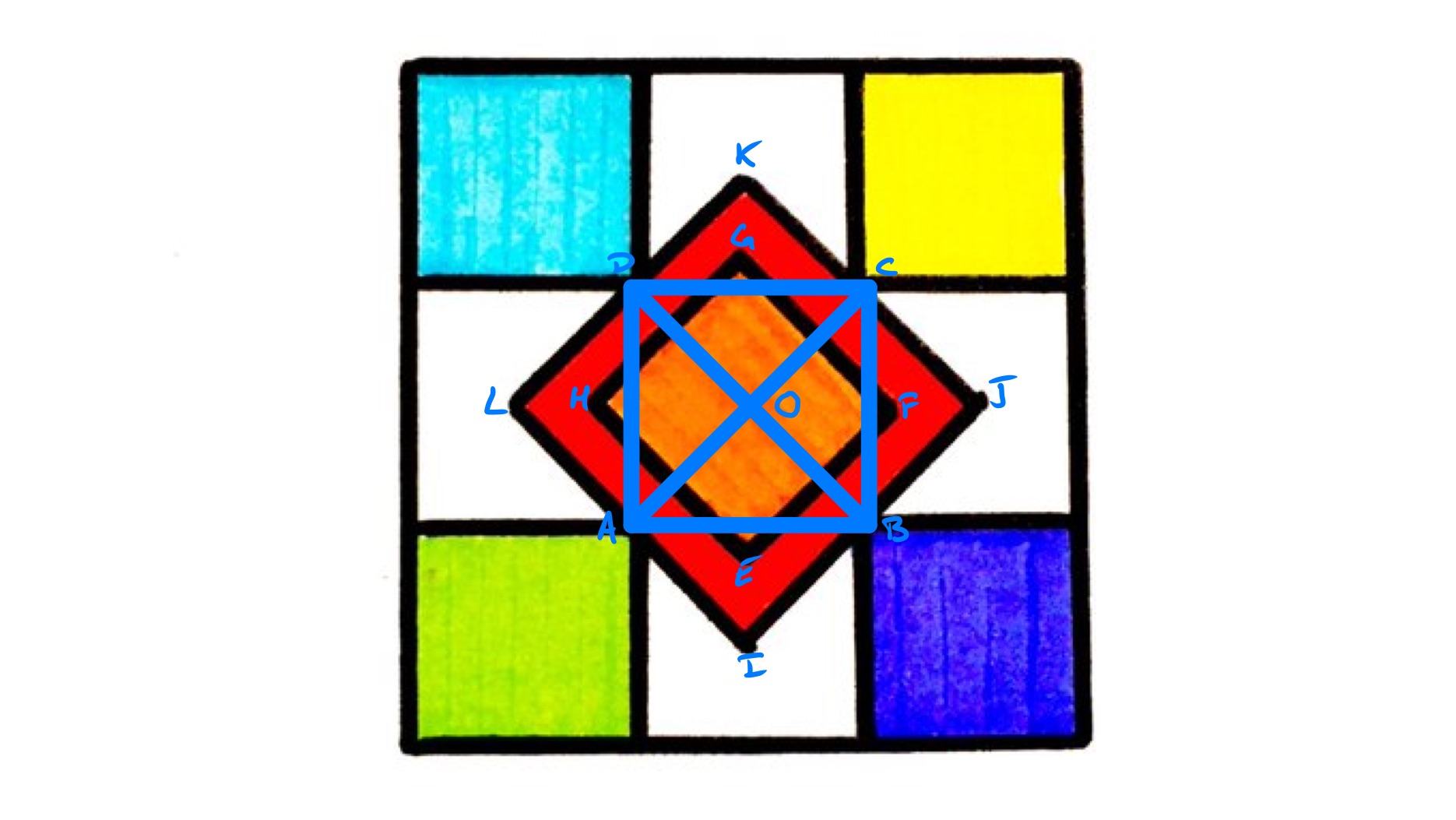
As every basic shape in the diagram is a square, the points labelled $A$, $B$, $C$, and $D$ where the re square meets the corner squares are the midpoints of the sides of the red square. The triangles $D K C$ and $D O C$ are congruent so they have the same area. Following this through for the other three pairs shows that the square $A B C D$ has half the area of $I J K L$. Since this is also true for the orange square, $A B C D$ and the orange square must be congruent. This means that the outer square is divided into a $3 \times 3$ pattern of smaller squares, each of the size of the orange square. The area of the full square is therefore $9$ times that of a small square, and there are $6$ shaded regions, so $\frac{2}{3}$rds of the outer square is shaded.