Notes
two squares iii solution

Solution to the Two Squares III Puzzle

Solution by Dissection, Area of a Square, and Area of a Triangle

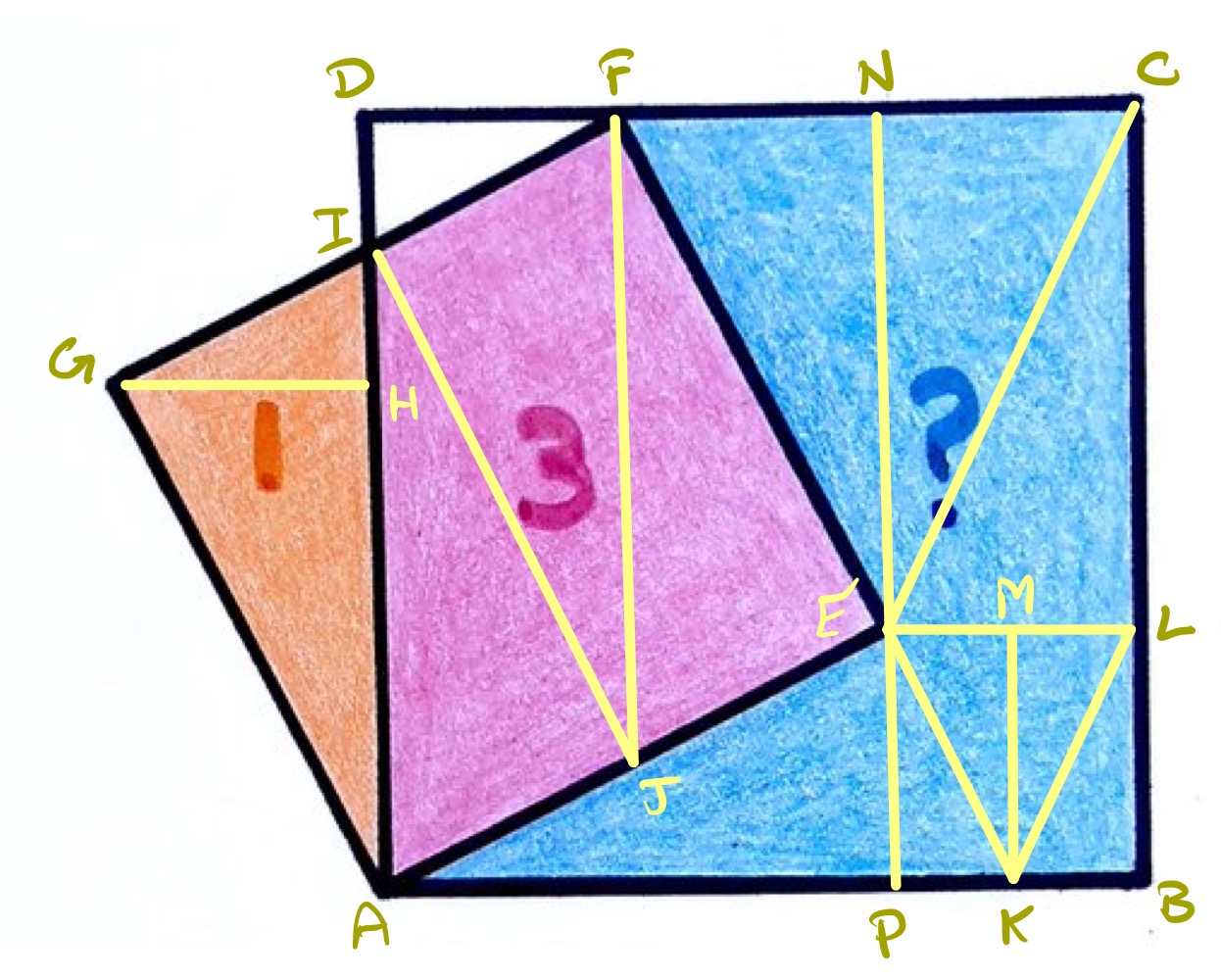
In the diagram above, the additional points are as follows:

• $H$ is so that $G H$ is perpendicular to $A D$,
• $J$ is so that $I J$ is parallel to $G A$,
• $N$ and $P$ are so that $N P$ passed through $E$ and is perpendicular to $D C$,
• $L$ is so that $E L$ is perpendicular to $C B$,
• $K$ is so that $E K$ is the continuation of $F E$,
• $M$ is so that $M K$ is perpendicular to $A B$.

Since the tilted square, $A E F G$, has total area $4$, its side length is $2$. Then $A G I$ is a right-angled triangle with area $1$ and $A G$ has length $2$, so $G I$ must have length $1$. This means that $I$ is the midpoint of $G F$, and then that $I$ is also the midpoint of $H D$.

Since $I J$ is parallel to $G A$, this means that $J$ is also the midpoint of $A E$, and then that $J F$ is parallel to $A I$. So the decomposition shown of the purple region is into three congruent triangles, each of area $1$.

Since $E K$ is the continuation of $F E$, triangle $A E K$ is right-angled. Then as $A E$ has the same length as $A G$, and angles $K \hat{A} E$ and $I \hat{A} G$ are the same, triangles $A E K$ and $A G I$ are congruent. Therefore, line segments $A K$ and $A I$ have the same length, so since $A D$ and $A B$ are sides of the same square, line segments $K B$ and $I D$ have the same length. Then line segment $B L$ has the same length as $G H$, so triangle $K B L$ is congruent to triangle $I H G$.

The congruency between $A G I$ and $A E K$ takes $H$ to $P$, so triangle $E P K$ is also congruent to triangle $G H I$, meaning that line segment $P K$ also has the same length as $G H$, and so $K$ is the midpoint of $P B$. Since the lengths of $A G$ and $G I$ are in the ratio $2 : 1$, this also holds for $E P$ and $P K$, meaning that $E P$ and $P B$ have the same length, so then line segment $E L$ has the same length as $G H$.

Triangle $E N F$ is right-angled, with $E N$ parallel to $A H$ and $E F$ parallel to $A G$ and of the same length. Therefore, triangle $E N F$ is congruent to triangle $A G H$. Triangle $E N C$ is then also right-angled, shares $E N$ with triangle $E N F$, and line segment $N C$ is the same length as line segment $E L$, which is the same length as $G H$. Therefore, $E N C$ is also congruent to $A H G$. Since $E L C N$ is a rectangle, triangle $E L C$ is also congruent to triangle $A H G$.

In summary, triangles $E N F$, $E N C$, and $E L C$ are all congruent to triangle $A G H$; triangles $E M K$, $L M K$, $L B K$ are all congruent to triangle $G H I$; and triangle $A E K$ is congruent to triangle $A G I$. The three smallest pair with the three middle to create regions of area $1$; then since this is also the area of triangle $A E K$ this gives a total area of $4$.