Notes
two squares and an equilateral triangle ii solution
Solution to the Two Squares and an Equilateral Triangle II Puzzle
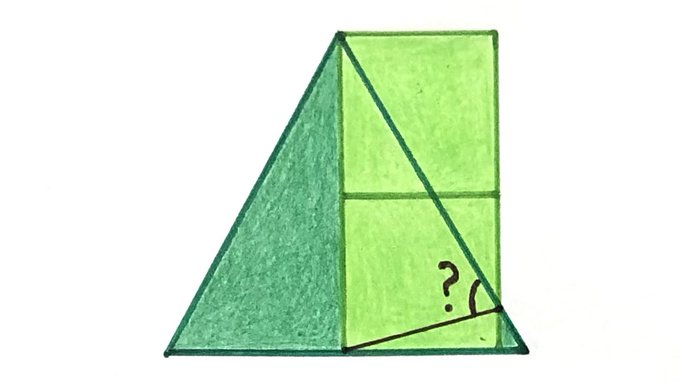
Two squares and an equilateral triangle. What’s the angle?
Solution by Pythagoras' Theorem, Lengths and Angles in an Equilateral Triangle, and Angles in an Isosceles Triangle
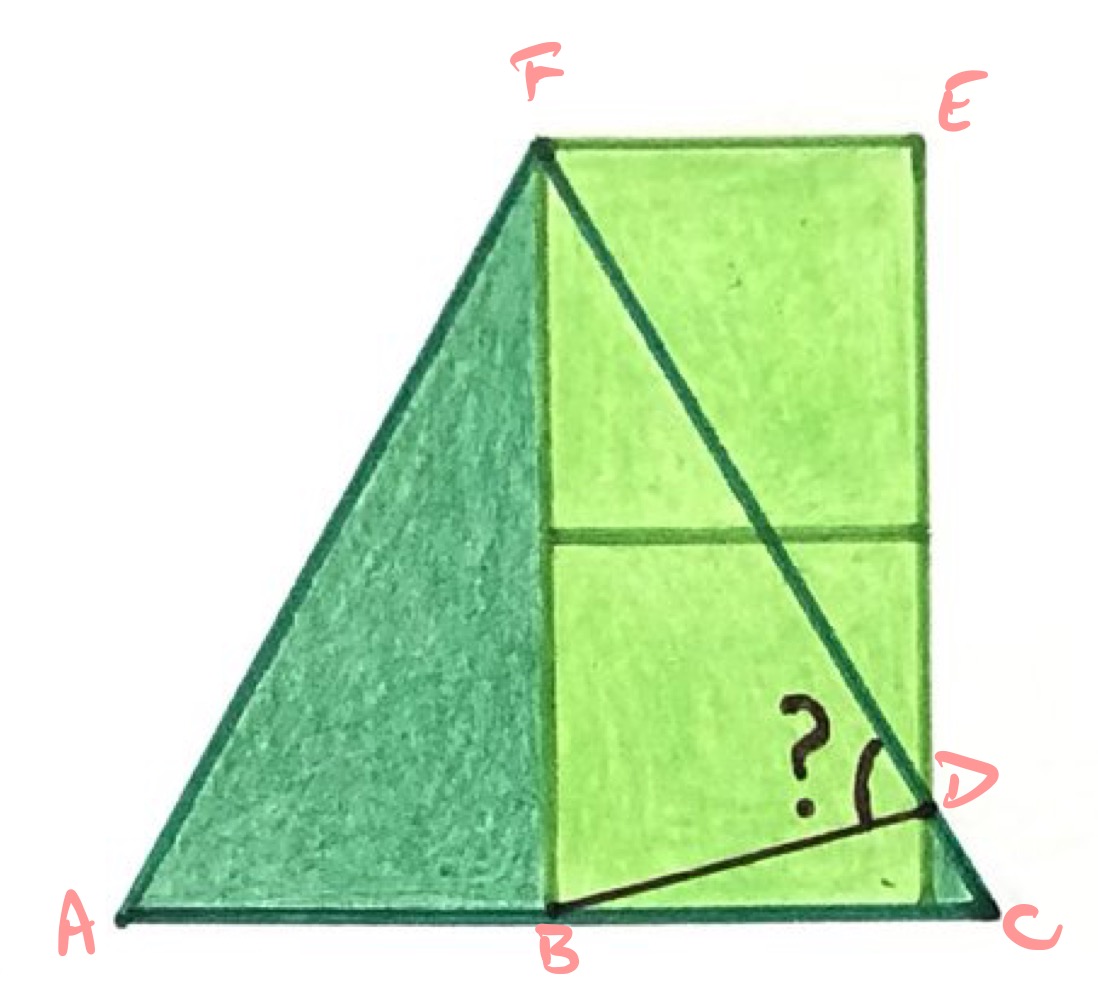
Label the diagram as above.
Let have length , then from the lengths in an equilateral triangle, has length so the side length of the squares is . Angles and are alternate angles so is . This means that triangle is half an equilateral triangle, so has length times that of , so has length . Applying Pythagoras' Theorem to triangle shows that the length of is the square root of:
Hence has length which is the same as the length of . Therefore, triangle is isosceles. Since angle is , this means that angle is .
Solution by Lengths and Angles in an Equilateral Triangle, and Angles in an Isosceles Triangle
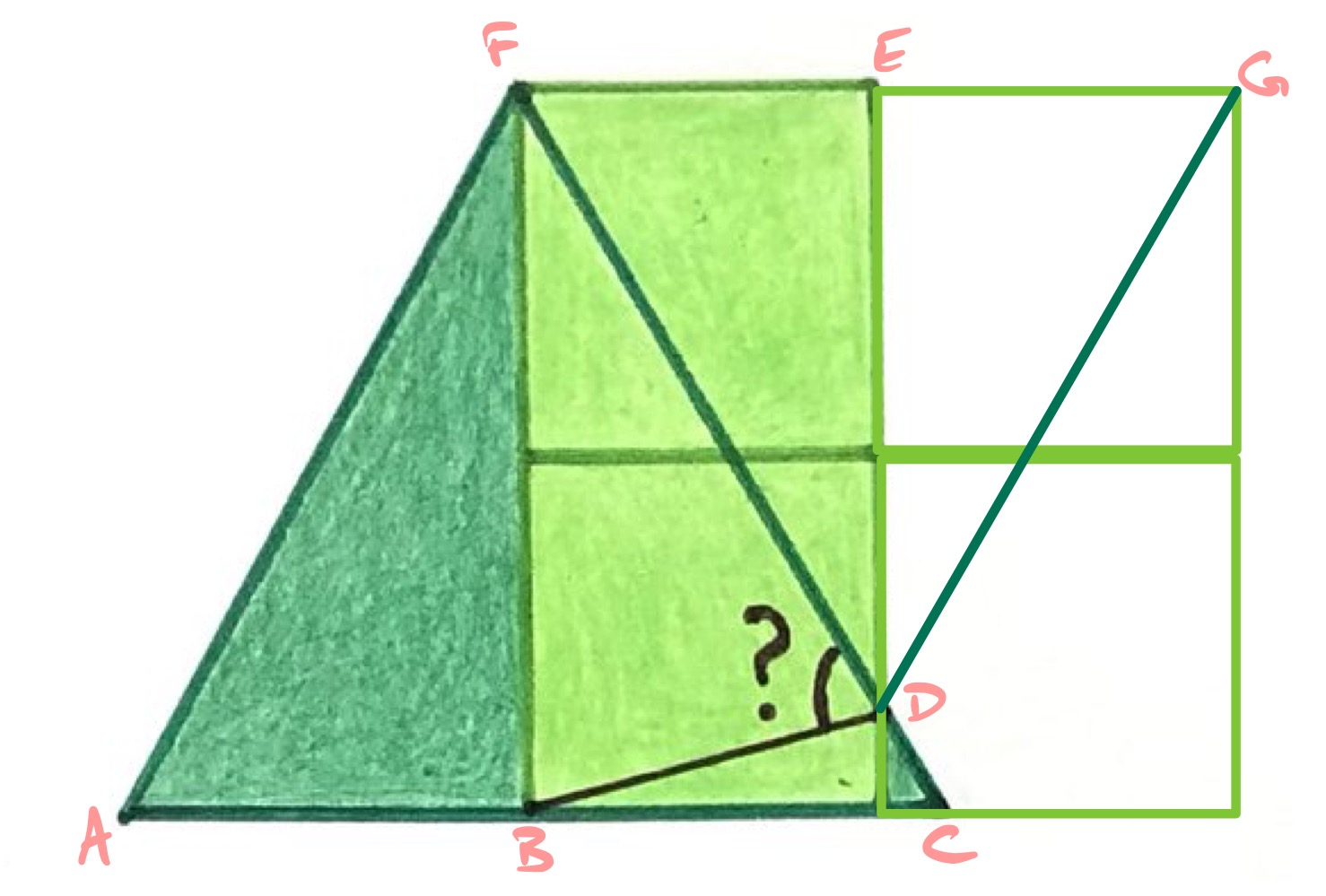
Extend the diagram by adding two more squares as above, and label the diagram as shown.
By symmetry, triangle is isosceles. Then since angles and are corresponding angles they are the same, so angle is . This means that triangle is actually equilateral and so has the same length as , which has the same length as .
Hence triangle is isosceles and since angle is , angle is .