Notes
two rectangles overlapping a circle solution
Solution to the Two Rectangles Overlapping a Circle Puzzle
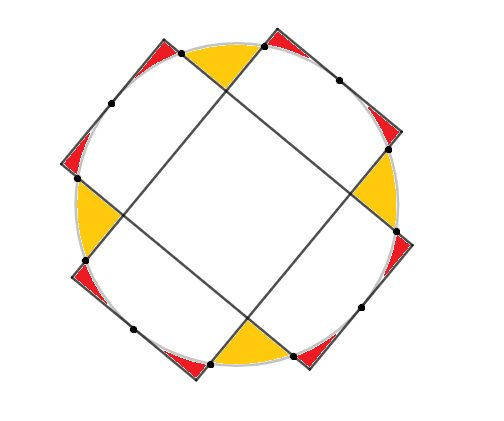
Which is the larger area: red or orange? The points around the circumference are evenly spaced.
Solution by Area of a Circle, Area of a Rectangle, and Lengths in a Regular Hexagon
As this is a comparison of areas, let us set the radius equal to unit. Then the red area is the area of the cross (formed from two overlapping rectangles) without the white region, and the yellow area is the area of the circle without the white region. Therefore, to compare the red and yellow areas it is sufficient to compare the area of the circle with the area of the cross.
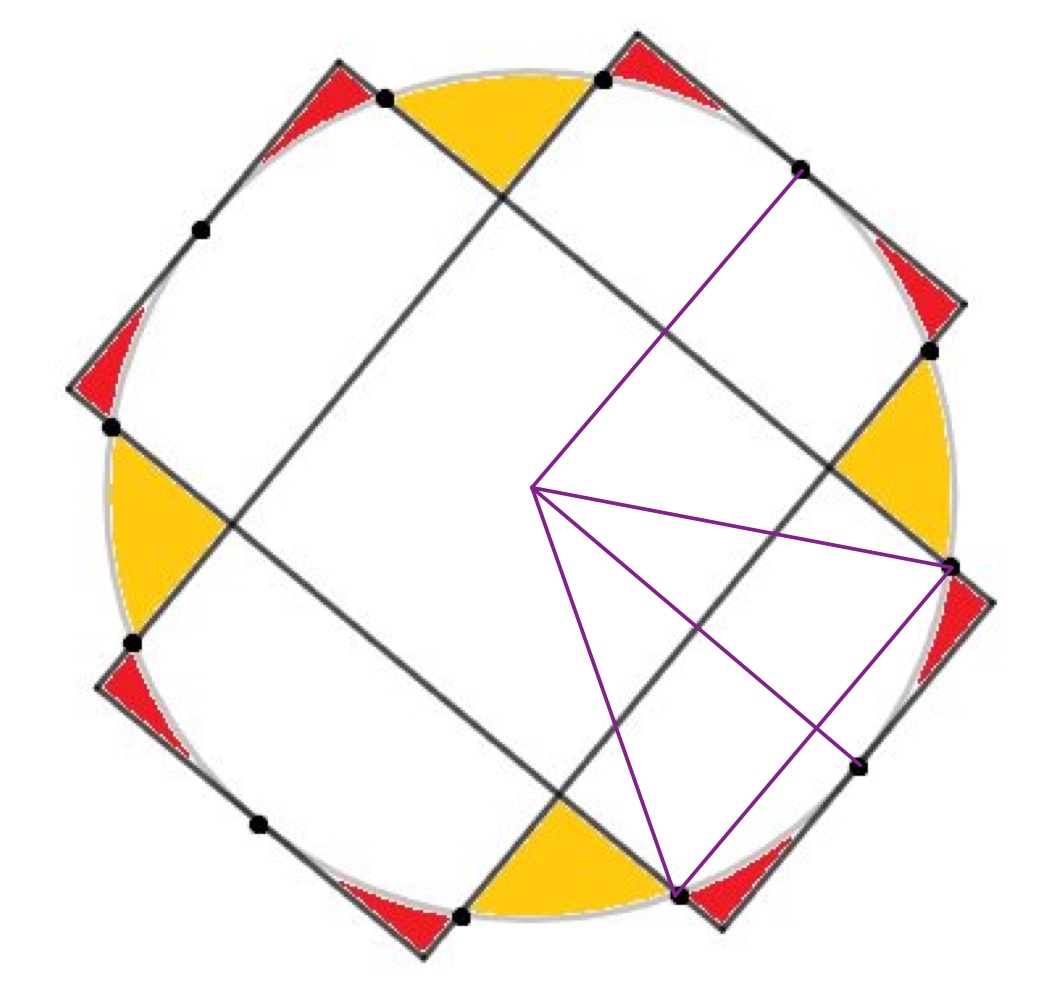
As the dots are evenly spaced, and there are twelve of them, joining every other dot forms a regular hexagon. One segment of this, as shown, is an equilateral triangle meaning that the height of the rectangle is equal to the radius of the circle. This means that the dimensions of the rectangle are , and the central square has dimensions . So the area of the cross is .
Since the area of the circle is and , the yellow area is larger than the red area.
For completeness, to work out the white area then split the white part of one rectangle into two sectors and two triangles. Each sector has area . Each triangle has base and height so has area . The white area inside one rectangle has area so the area of the full white region is:
Therefore the red area is:
and the yellow area is:
The difference between these is as before.