Notes
two quarter circles and a circle solution

Solution to the Two Quarter Circles and a Circle Puzzle

Solution by Pythagoras' Theorem and Properties of an Isosceles Right-Angled Triangle

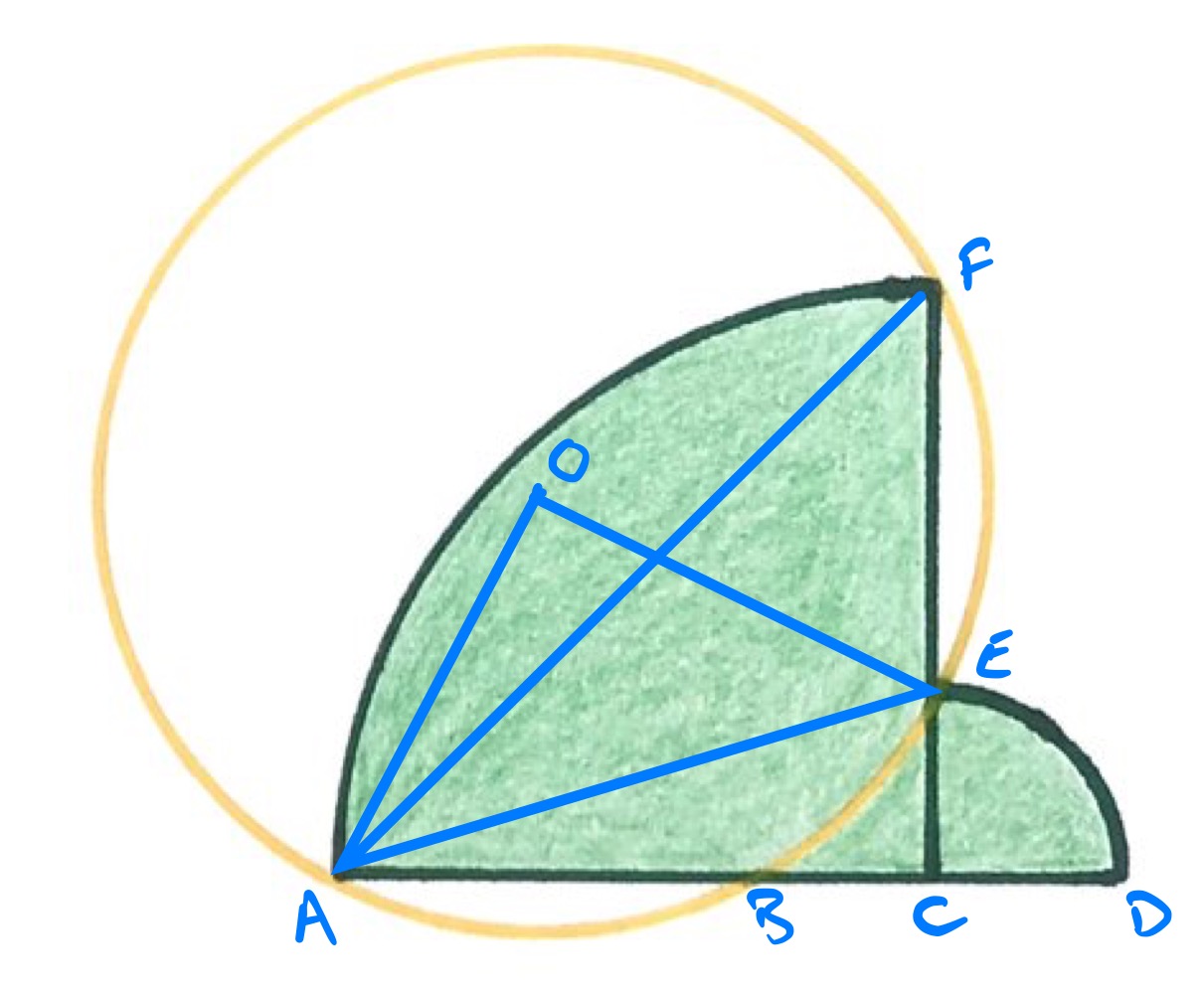
In the diagram above, $O$ is the centre of the circle.

Angle $A \hat{F} E$ is $45^\circ$, since triangle $A F C$ is an isosceles right-angled triangle. Therefore, as the angle at the centre is twice the angle at the circumference, angle $A \hat{O} E$ is $90^\circ$. This means that triangle $A O E$ is also an isosceles right-angled triangle, so the length of $A E$ is $\sqrt{2}$ times the length of $O A$, so is $4 \sqrt{2}$.

Let the radii of the circles be $R$ and $r$, then applying Pythagoras' theorem to triangle $A C E$ shows that:

The total area of the two quarter circles is therefore:

Solution by Invariance Principle

The sizes of the two quarter circles can vary.

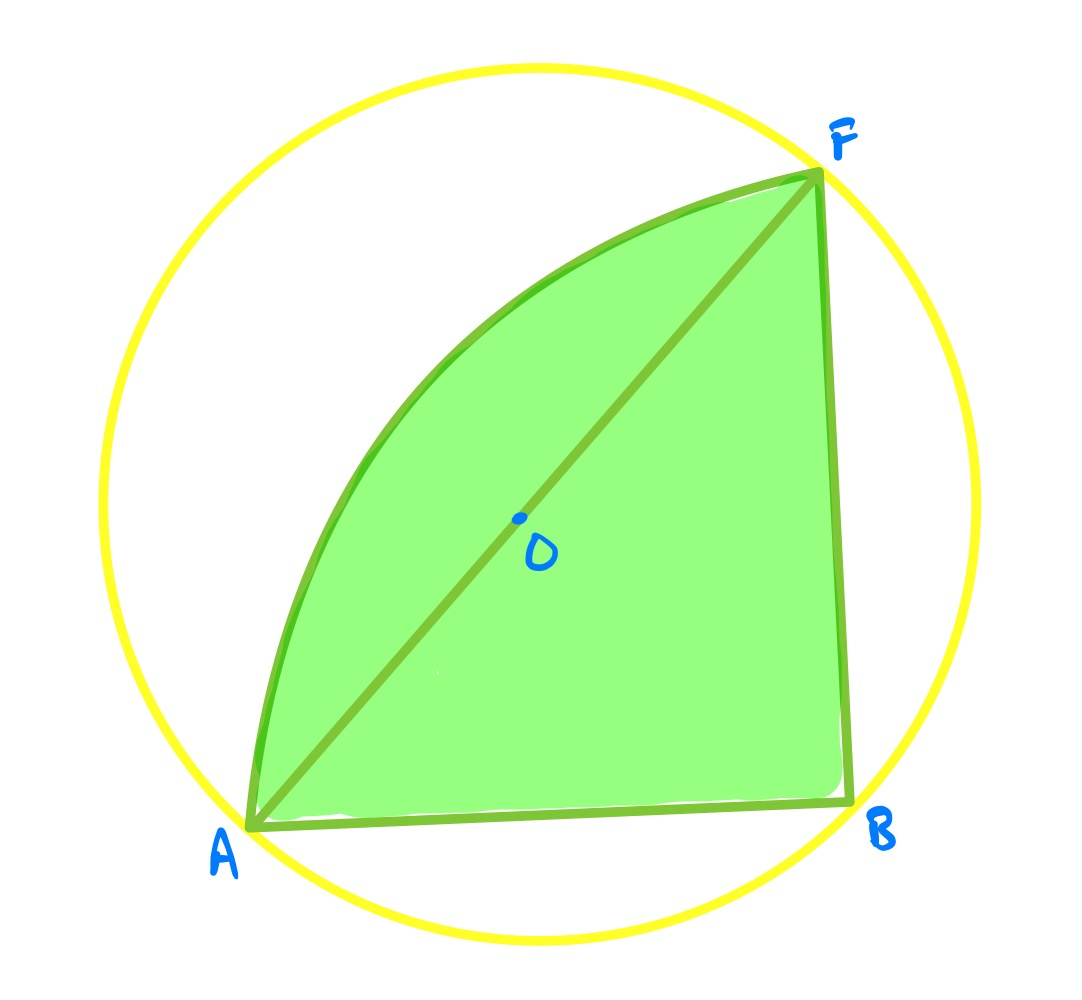
At one extreme, the smaller circle has shrunk down to zero size. In this case, $A F$ is a diameter of the circle so has length $8$. As triangle $A B F$ is isosceles and right-angled, $F B$ has length $\frac{8}{\sqrt{2}} = 4 \sqrt{2}$ so the quarter circle has area:

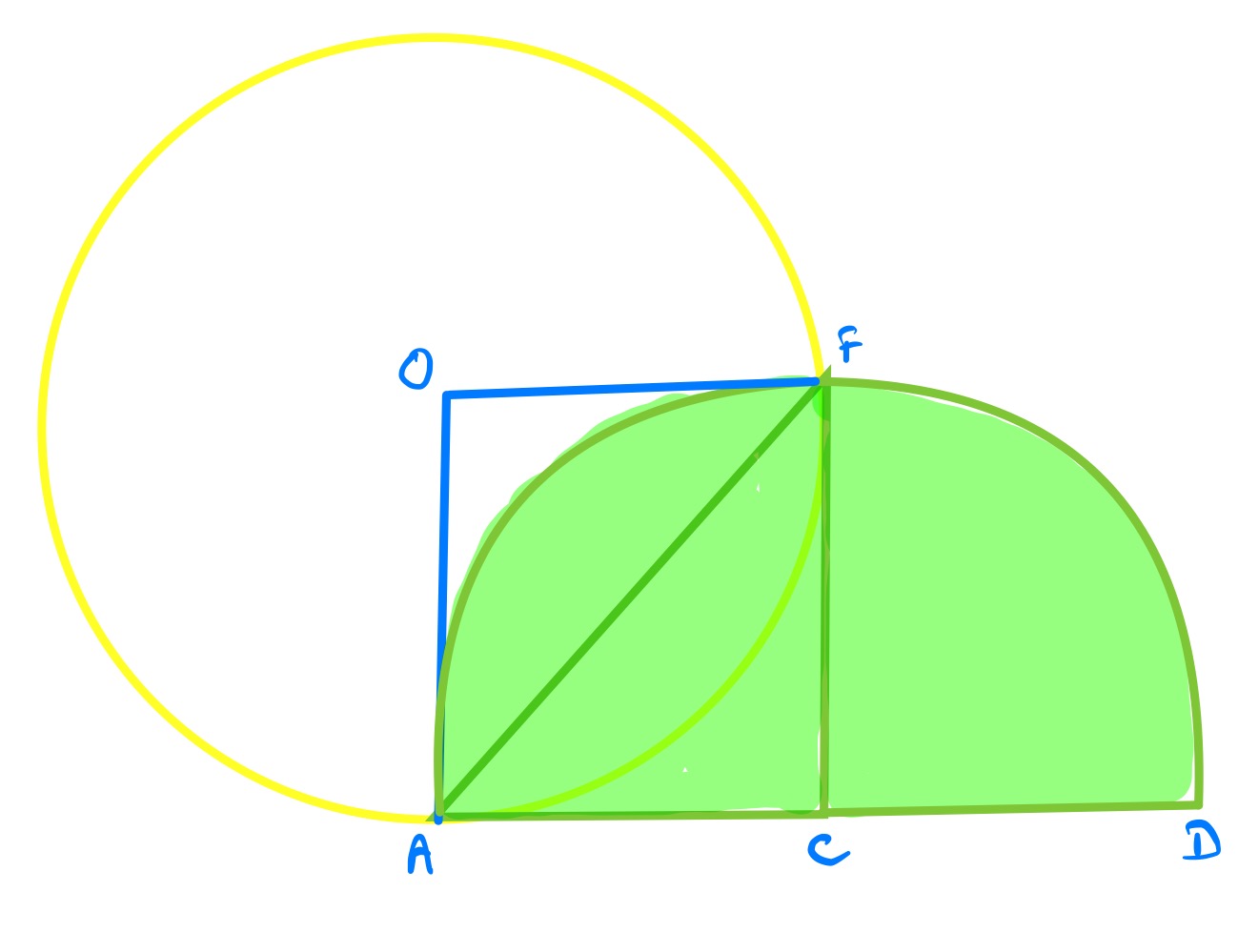
In this version, the two quarter circles have the same size. Then $A C F O$ is a square, so the quarter circles have the same radius as the circle, so have area: