Notes
two equilateral triangles ii solution
Solution to the Two Equilateral Triangles II Puzzle
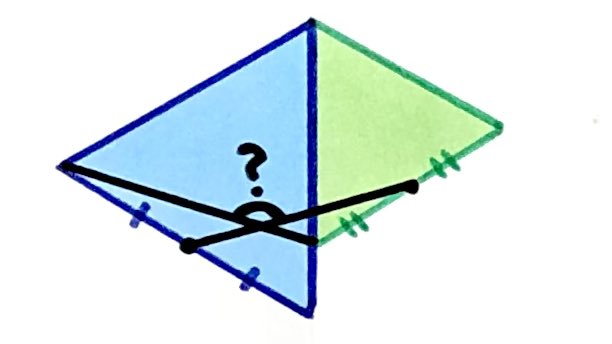
Both triangles are equilateral. What’s the angle?
Solution by Transformations and Lengths and Angles in an Equilateral Triangle
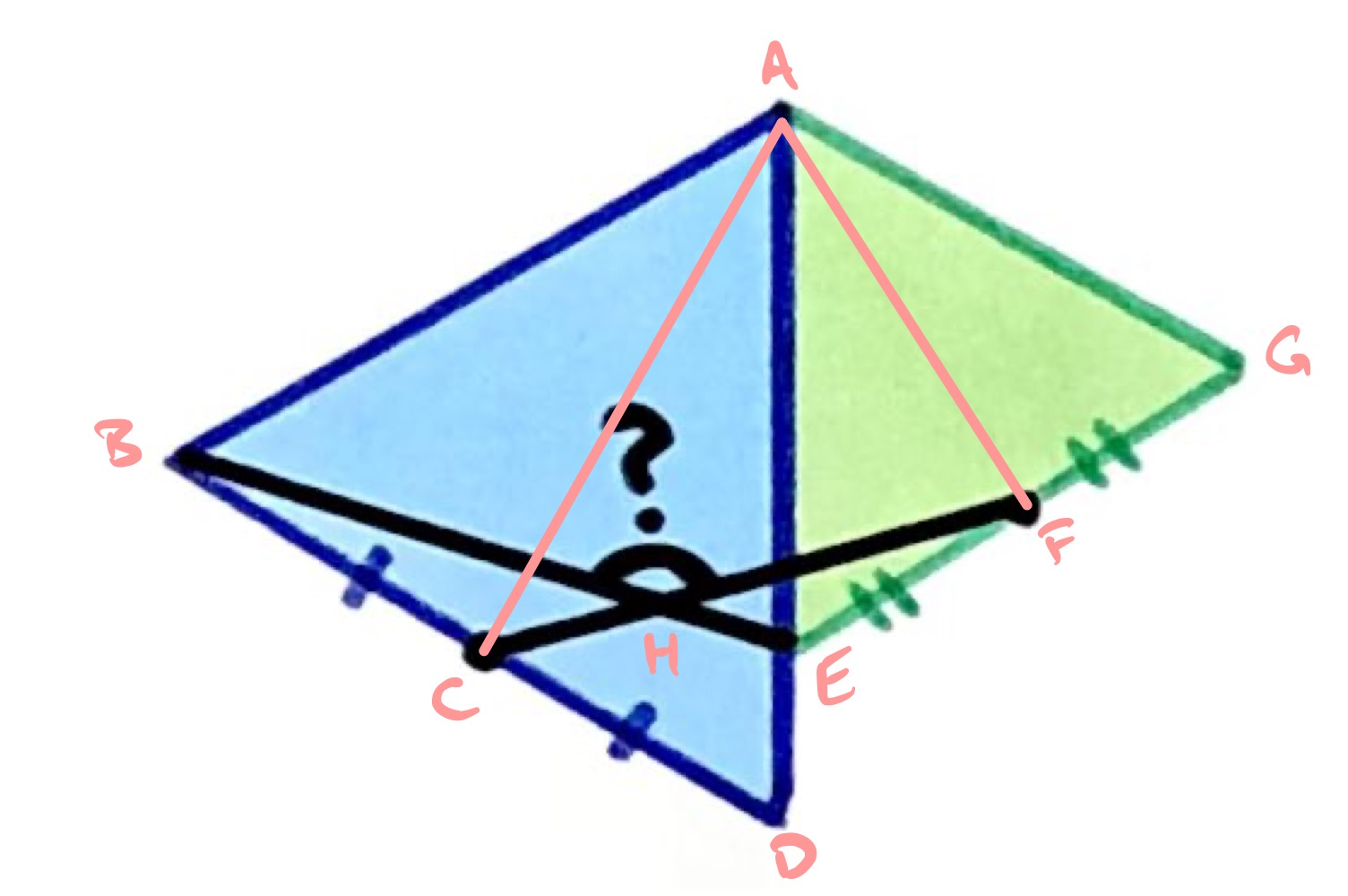
Consider the diagram labelled as above.
Triangle is similar to triangle by a rotation of anticlockwise about with a scaling with scale factor . This comes from the lengths and angles in an equilateral triangle. In particular, is at angle to .
The requested angle is the obtuse angle , which is then .
Solution by Invariance Principle
The relative sizes of the triangles is not fixed, so they can be drawn at different ratios.
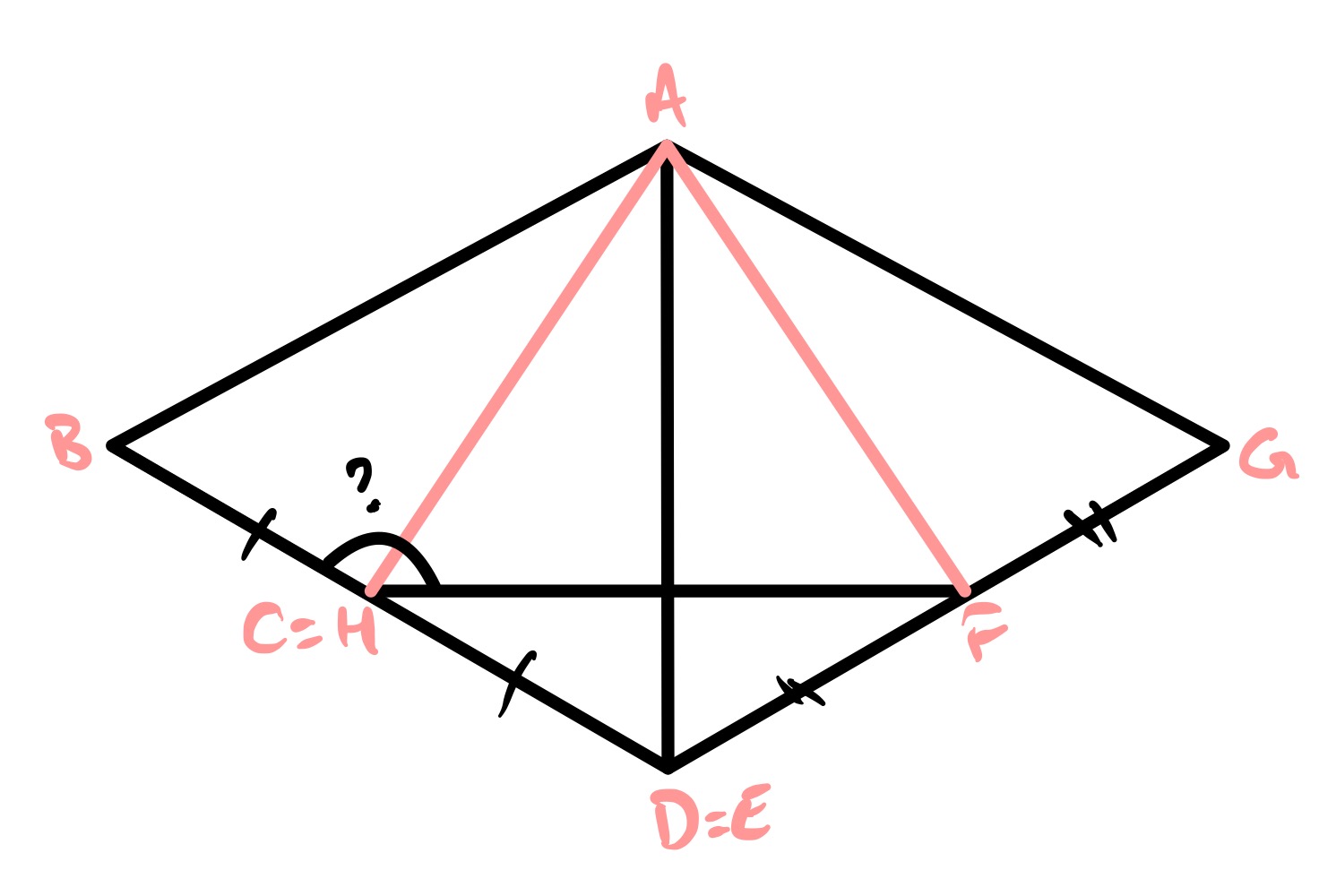
In this first version the two triangles are the same size, so line segments and are the same length and thus triangle is equilateral triangle. Hence angle , so since angle , the requested angle is .
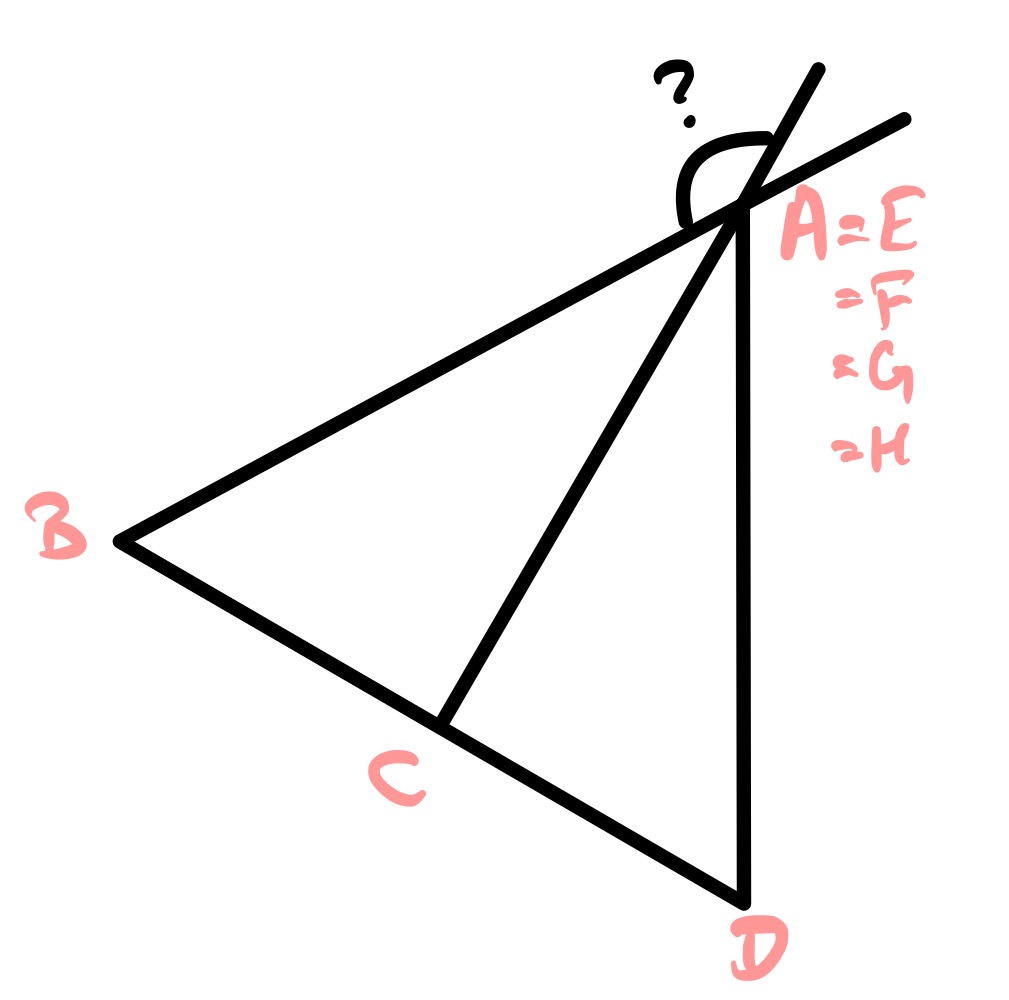
In the second version the right-hand triangle is shrunk to a point, so , , , , and coincide. To get the requested angle we extend and , then as , the requested angle is .