Notes
two circles in a triangle solution
Solution to the Two Circles in a Triangle Puzzle
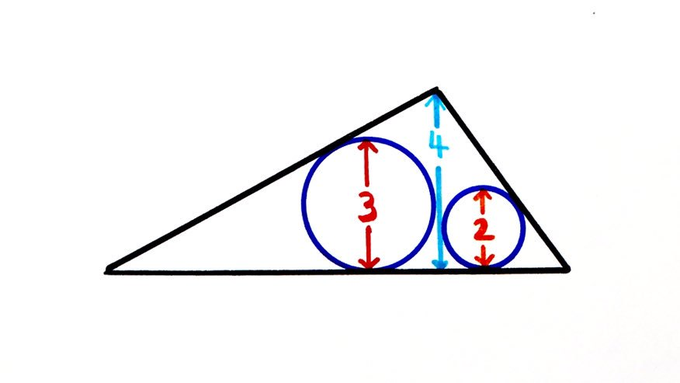
What’s the area of this triangle?
Solution by Angle Between a Radius and Tangent and Pythagoras' Theorem
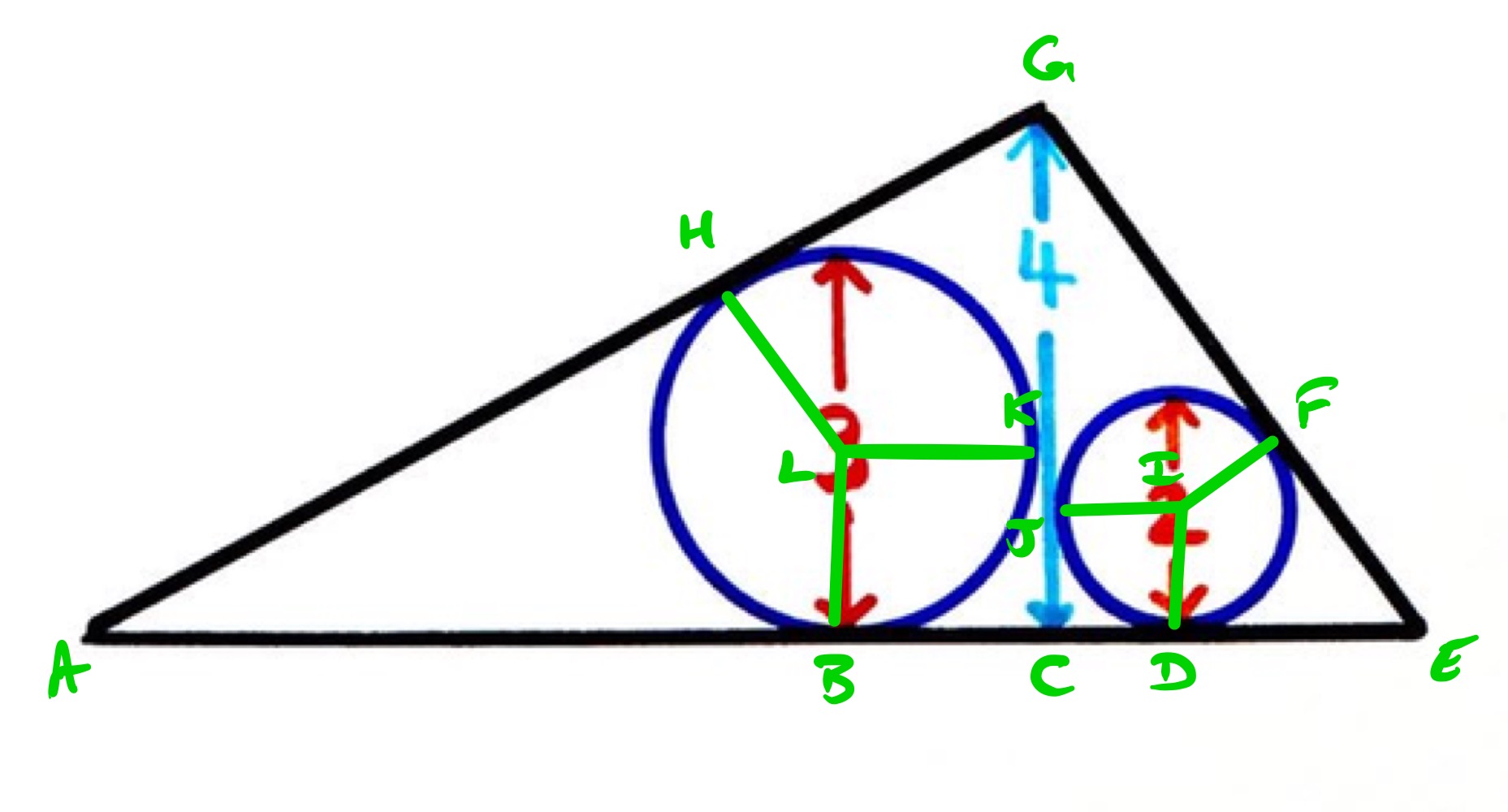
Let the points be labelled as above.
Consider the right-hand triangle, , with its in-circle of radius . The length of is , and is perpendicular to since the angle between a radius and tangent is , so has length . By symmetry, also has length . Let have length , so then also has length , and the sides of the right-angled triangle are therefore , , and . Applying Pythagoras' theorem shows that:
Now consider the left-hand triangle, . Let have length , then by a similar argument the lengths of are , , and . Applying Pythagoras’ theorem again shows that:
Thus the length of is and so the area of the triangle is .