Notes
triangle and semi-circle in a circle solution

Solution to the Triangle and Semi-Circle in a Circle Puzzle

Solution by Lengths in an Equilateral Triangle and in a Circle

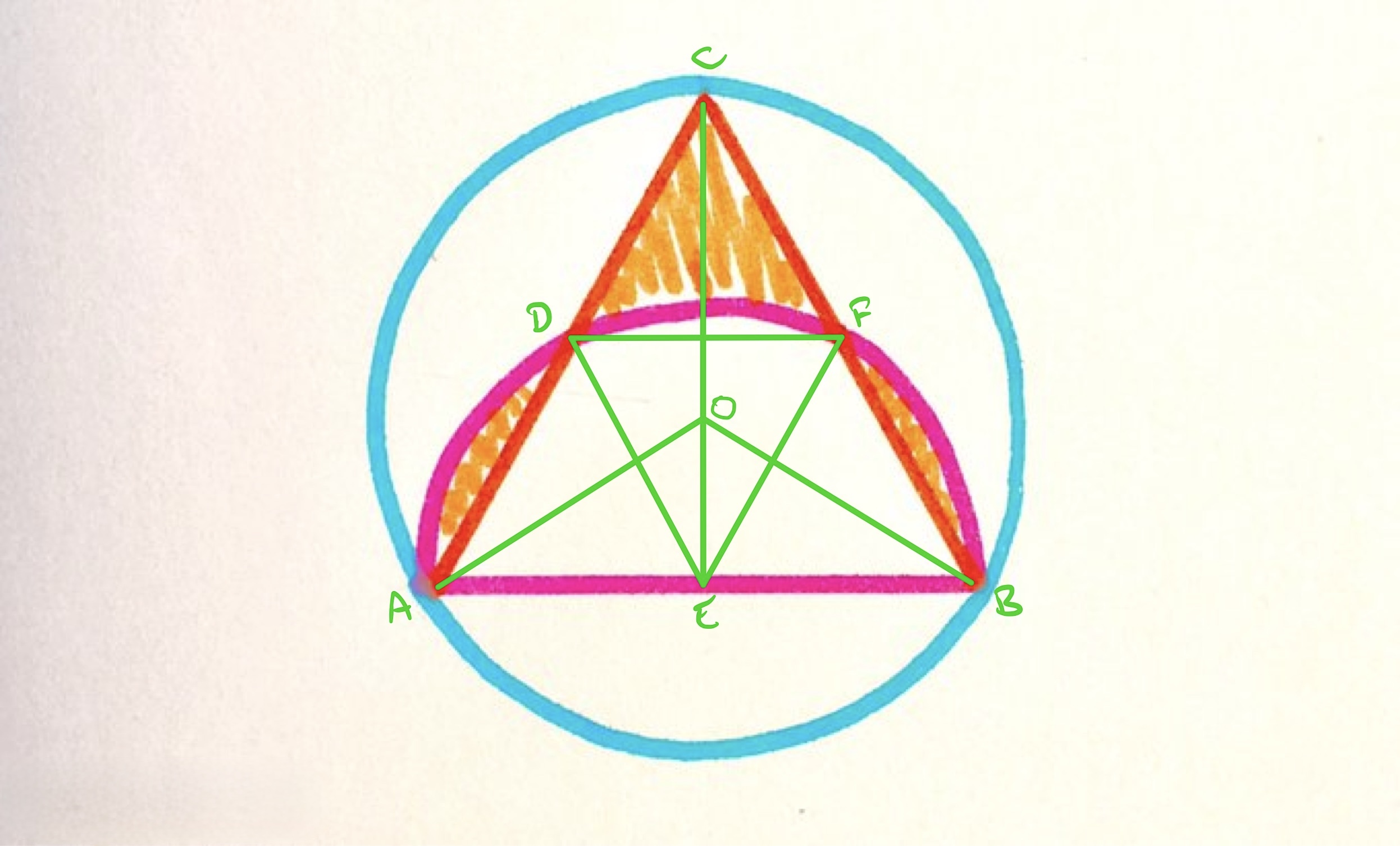
Consider the diagram as labelled above, in which $O$ is the centre of the circle and $E$ is the centre of the semi-circle.

As triangle $A B C$ is an equilateral triangle, angle $E \hat{A} D$ is $60^\circ$, and sides $A E$ and $D E$ are both radii of the semi-circle so are the same length, hence triangle $A E D$ is also an equilateral triangle. By a similar argument, so is triangle $B E F$, and then so must be triangle $D E F$.

This also establishes $D$ as the midpoint of $A C$ since $A D$ is the same length as $A E$, and $A C$ is the same length as $A B$. So triangle $C D F$ is also equilateral, and the four smaller triangles are all congruent.

The missing segment? $D F$ which is unshaded in triangle $C D F$ matches the shaded segment $F B$. Thus the top and right shaded parts together form a complete equilateral triangle. This equilateral triangle is congruent to triangle $A E D$, so the total shaded area is equivalent to the sector $A E D$.

Therefore the area of the shaded regions is one sixth of the area of circle with diameter $A B$. Using the relationship between the side length and height of an equilateral triangle, the radius of the semi-circle, $E B$, has length $\frac{\sqrt{3}}{2}$ times that of $O B$, which is the radius of the outer circle.

The area of the circle with radius $E B$ is therefore $\frac{3}{4}$ths of the area of the outer circle, and so the shaded regions have area $\frac{1}{6} \times \frac{3}{4} = \frac{1}{8}$th of the area of the full circle.