Notes
three triangles in a square solution
Solution to the Three Triangles in a Square Puzzle
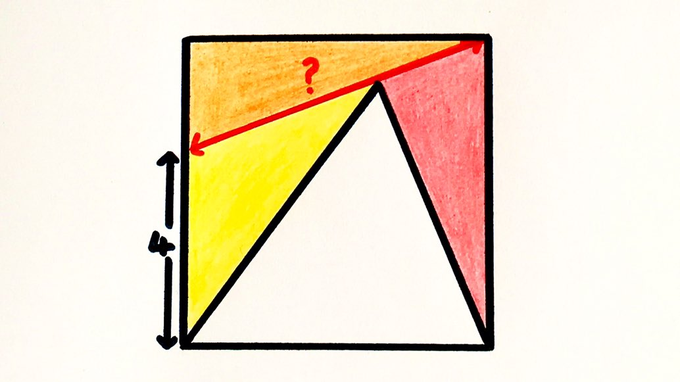
Inside this square are three triangles of equal area. How long is the red line?
Solution by Area of a Triangle and Pythagoras' Theorem
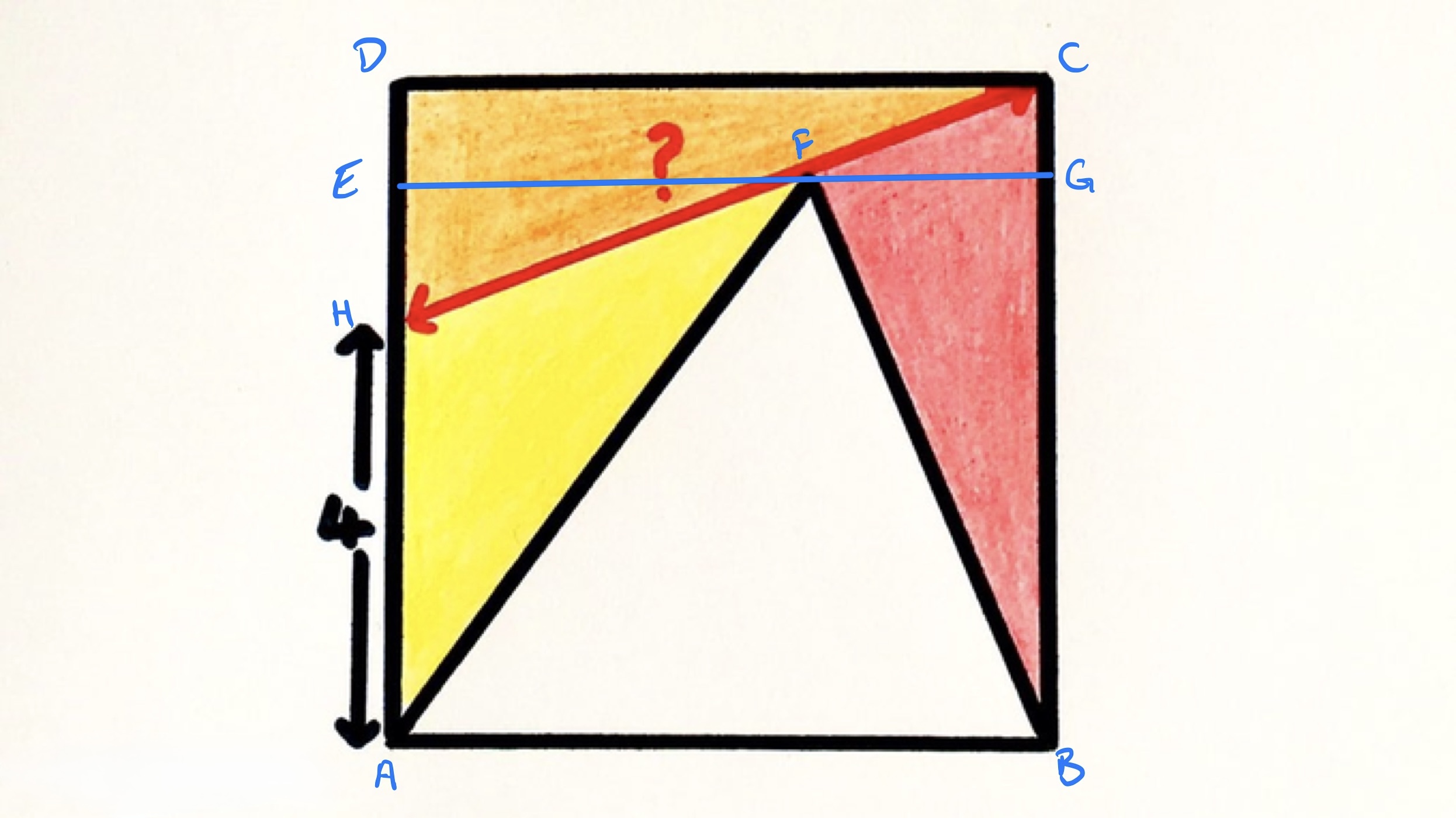
In the diagram above, is a straight line parallel to the side of the square.
Triangles and have the same area and the same length base since and are sides of the square, so by the formula for the area of a triangle their heights must be the same. Hence and have the same length.
Then since and make up one side of the square, which is the same length as , must have the same length as , namely . This means that the area of triangle is , and so this is the area of all the triangles.
Let be the side length of the square. Then has length , so since the orange triangle has area , we have: so .
Let be the length of . Applying Pythagoras' theorem to triangle shows that:
Hence .