Notes
three squares viii solution
Solution to the Three Squares VIII Puzzle
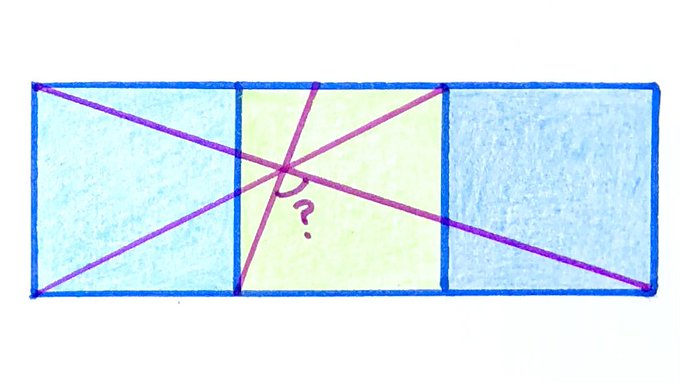
Three squares. What’s the angle?
Solution by Similar Triangles and Gradients of Perpendicular Lines
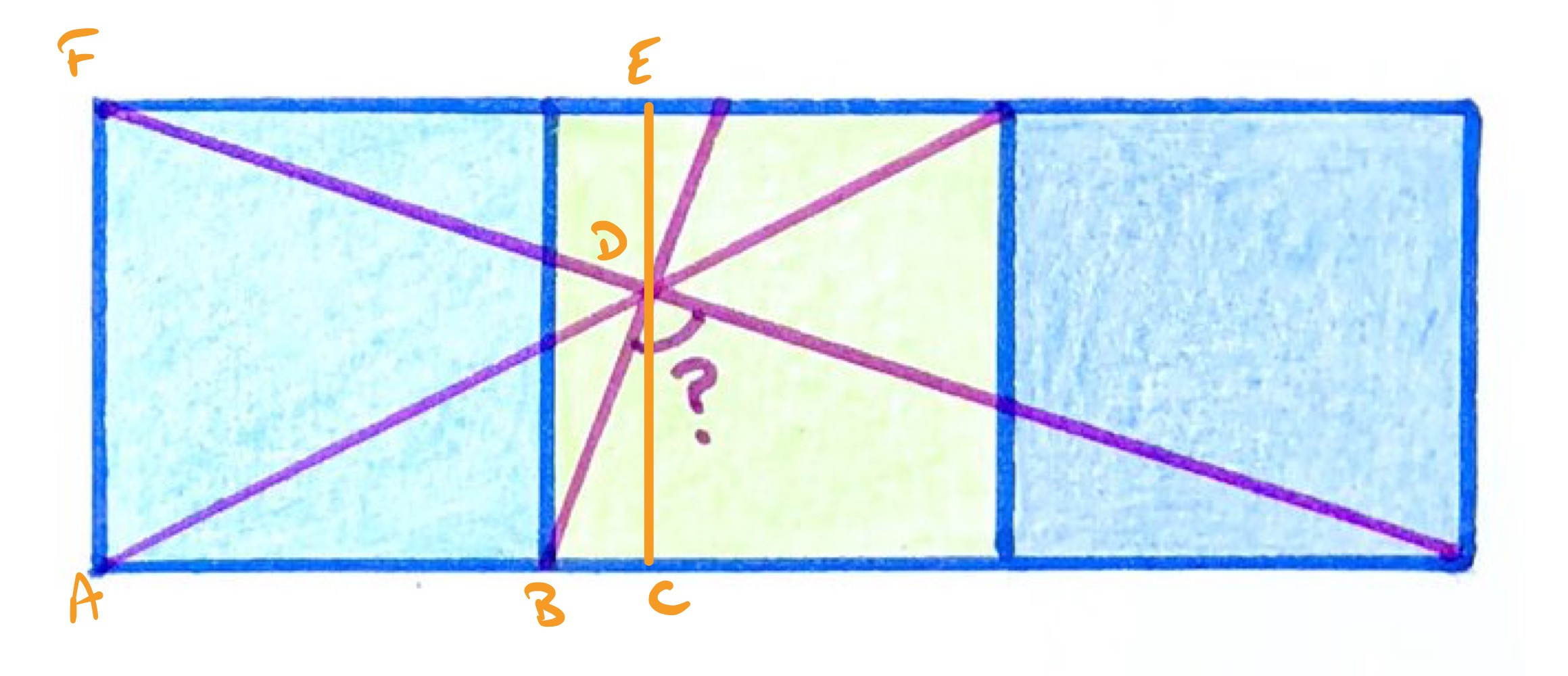
In the above diagram, line segment is vertical through the intersection point, .
By similarity, the lengths of and are in the ratio and the lengths of and are in the ration . Therefore, the lengths of and are in the ratio .
The length of is then of the side length of a square, so has length of the side length of a square. Then has length of the side length of a square.
The gradient of is therefore:
The gradient of is . Therefore and are perpendicular and so the angle is .