Notes
three squares in a circle solution
Solution to the Three Squares in a Circle Puzzle
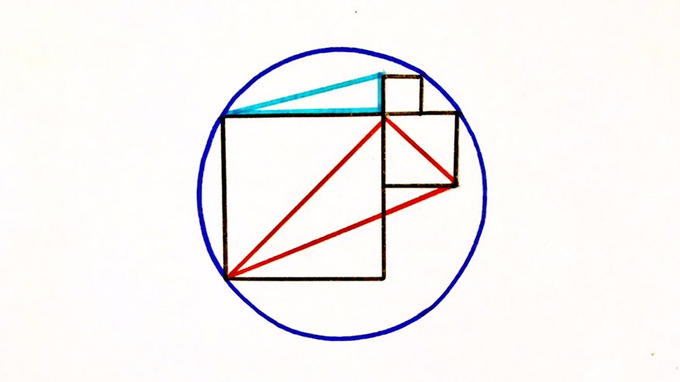
Three squares in a circle … If the blue triangle has area , what’s the area of the red triangle?
Solution by the Intersecting Chords Theorem, Lengths in a Square, and Area of a Triangle
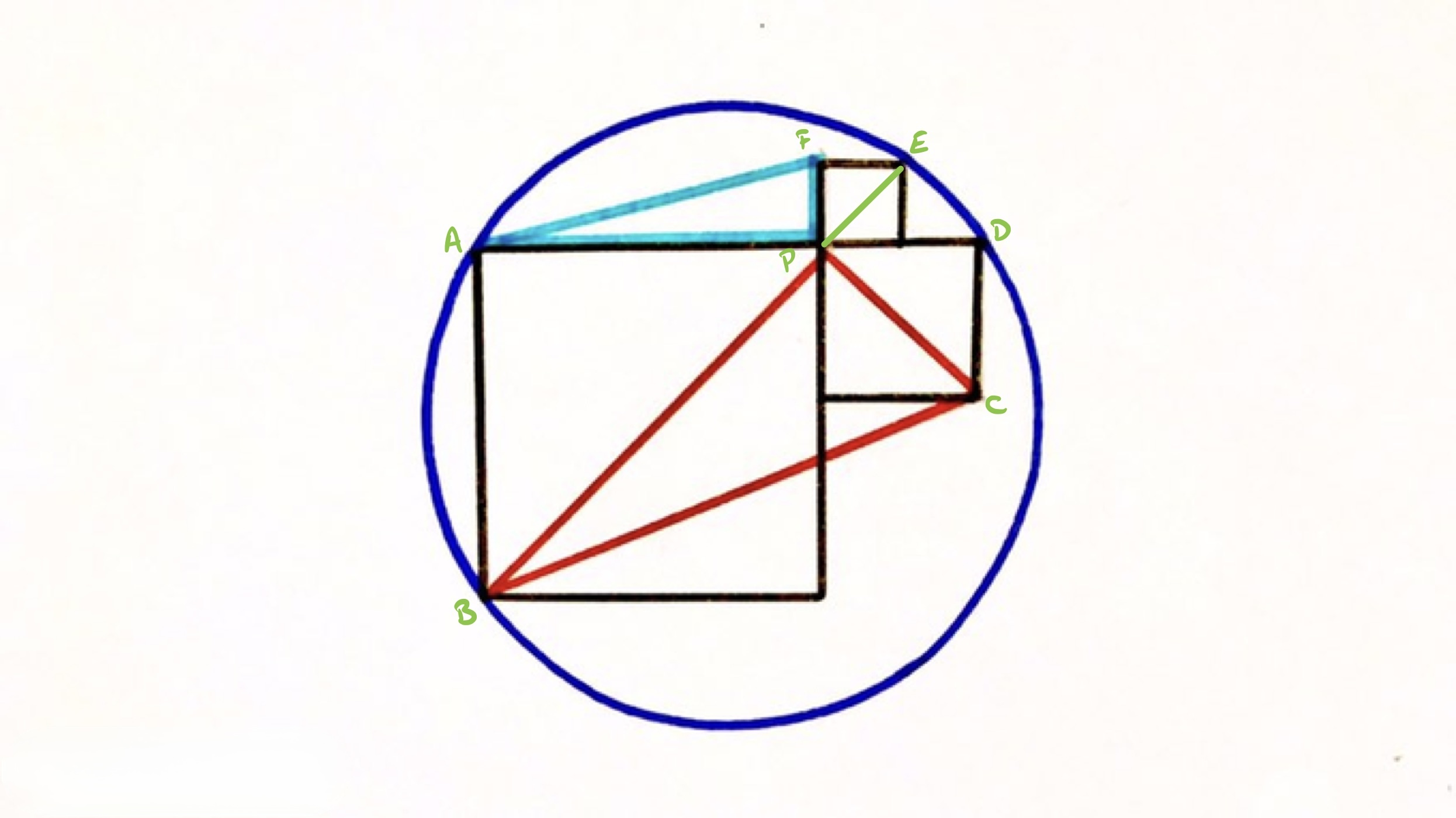
With the points as labelled in the diagram, and are chords of the circle that intersect at . Therefore, by the intersecting chords theorem, the lengths of the segments satisfy:
Now, is the diagonal of the square with as side length, so is . This means that must be . Since is the diagonal of the square with as side, and is the diagonal with as side:
Lastly, triangle is right-angled since and are diagonals of aligned squares.
Therefore, the area of triangle is: