Notes
three semi-circles in a rectangle solution
Solution to the Three Semi-Circles in a Rectangle Puzzle
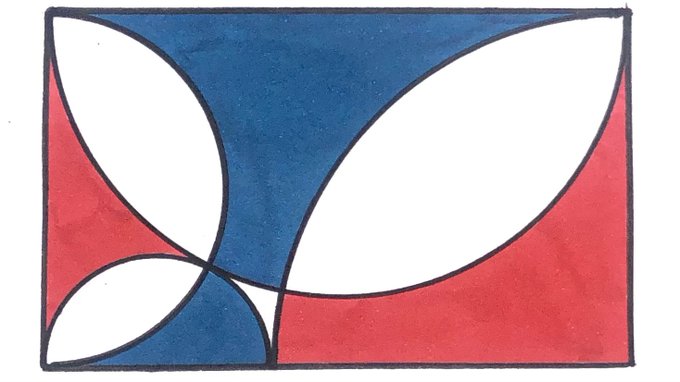
Is more of this rectangle red or blue?
Solution by Pythagoras' Theorem and the Area of a Circle
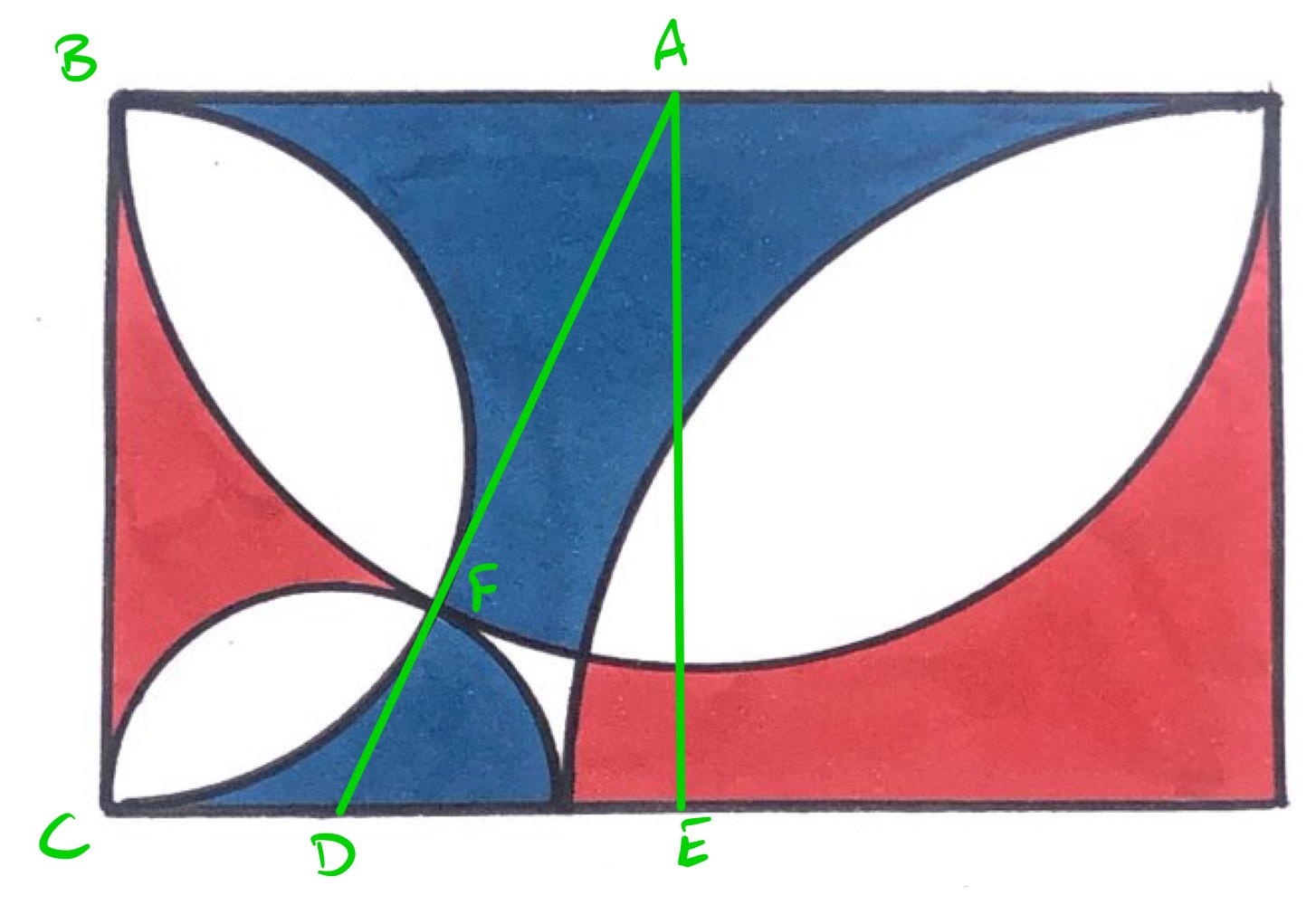
In the diagram above, is the midpoint of the upper edge so is the centre of the upper semi-circle, is the midpoint of the lower edge, and is the centre of the lower semi-circle.
Let be half of the width of the rectangle and half of its height. Then the radii of the various circles are:
- Upper semi-circle:
- Right quarter circle:
- Left semi-circle:
- Lower semi-circle:
By including the white petal regions into both the blue and red, the difference in the areas of the red and blue regions is the same as the differences in the corresponding partial circles.
The upper and lower semi-circles have area:
The left and right partial circles have area:
Triangle is a right-angled triangle with sides of lengths , , and . Applying Pythagoras' theorem yields:
Substituting in to the expression for the area of the upper and lower semi-circles, this shows that that area is:
which is exactly the area of the side circle segments. Hence the red and blue areas are the same.