Notes
three regular hexagons ii solution
Solution to the Three Regular Hexagons ii Puzzle
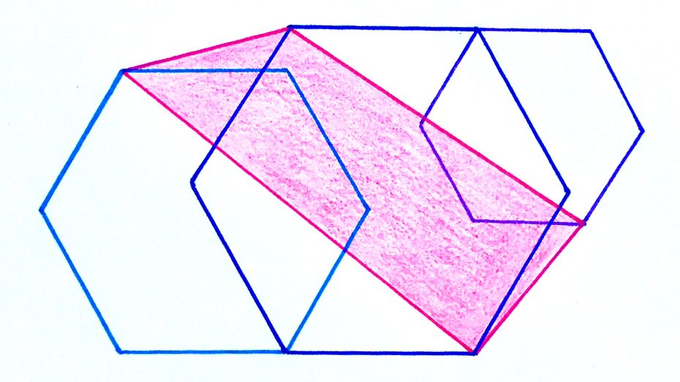
The largest of these regular hexagons has area . What’s the shaded area?
Solution by Area of a Triangle and Area of a Regular Hexagon
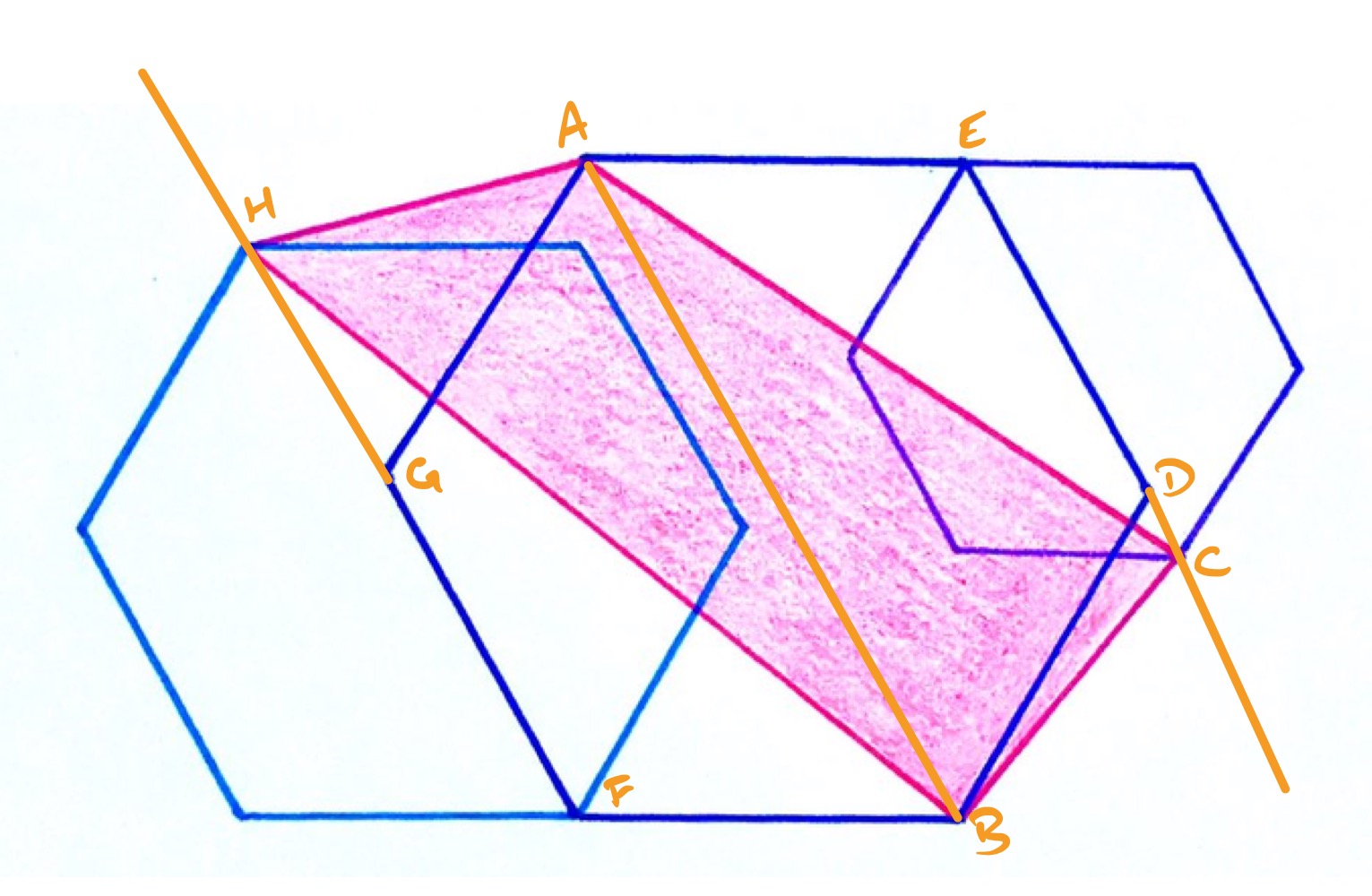
Consider the diagram with the points labelled as above. The purple region can be divided into two triangles, and . To find the area of each, consider them both as having base .
The left-hand hexagon can vary in size, but it remains anchored at point , so its diagonal remains on the line through and . This is parallel to , so the height of above is the same as that of above . So the area of triangle is the same as that of triangle .
A similar argument on the right-hand side shows that the area of triangle is the same as that of triangle .
Therefore, the purple region has the same area as rectangle , which, from the properties of a regular hexagon, is two thirds of the area of the central hexagon. Since that hexagon has area , the purple region has area .
Solution by Invariance Principle and Area of a Regular Hexagon
The left and right hexagons can vary in size, meaning that this problem can be solved by appealing to the invariance principle.
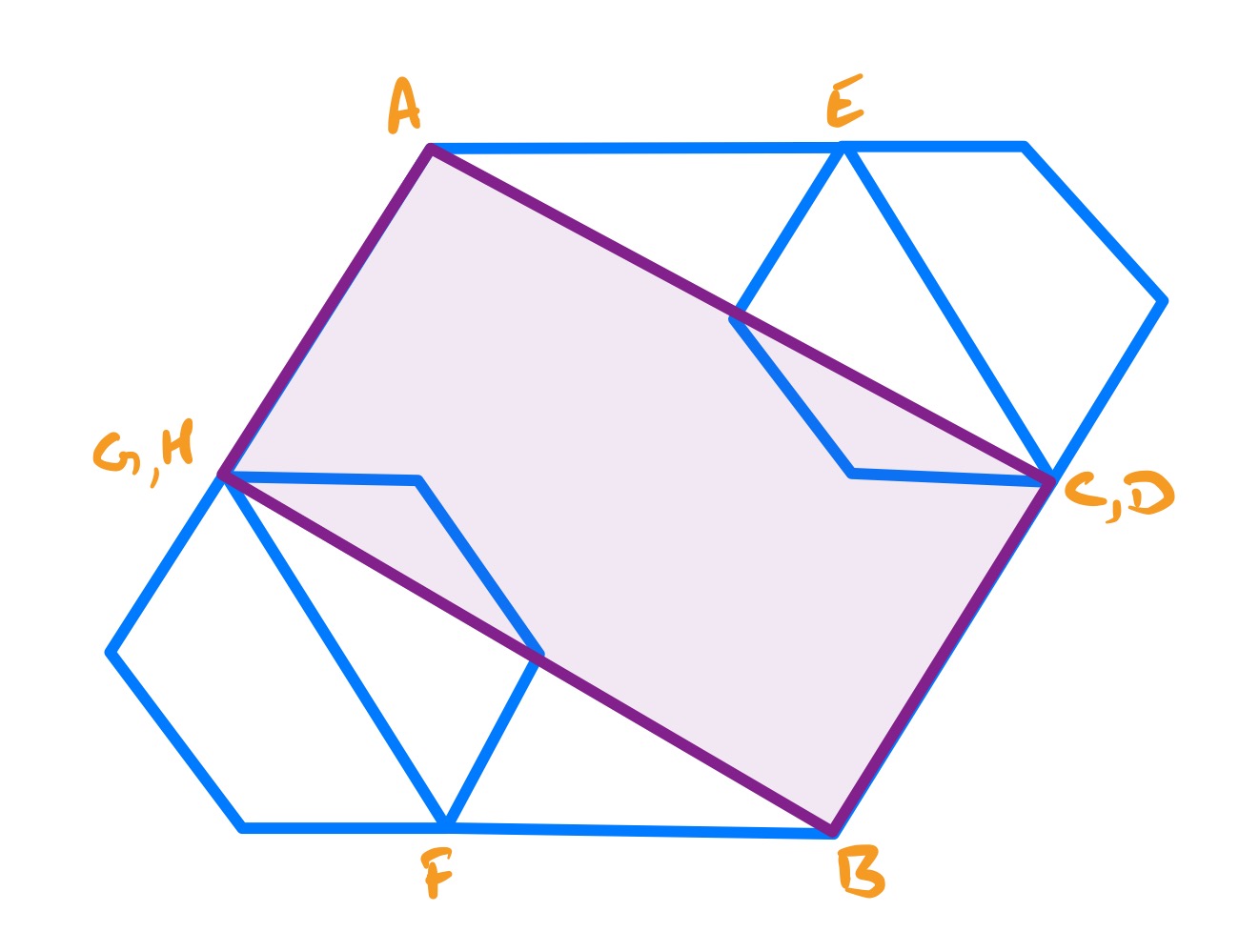
In this first configuration, the hexagons are sized so that their diagonals coincide with sides of the central hexagon, putting points and at and respectively. This means that the purple region coincides with a central rectangle of the hexagon, so its area is two thirds that of the hexagon.
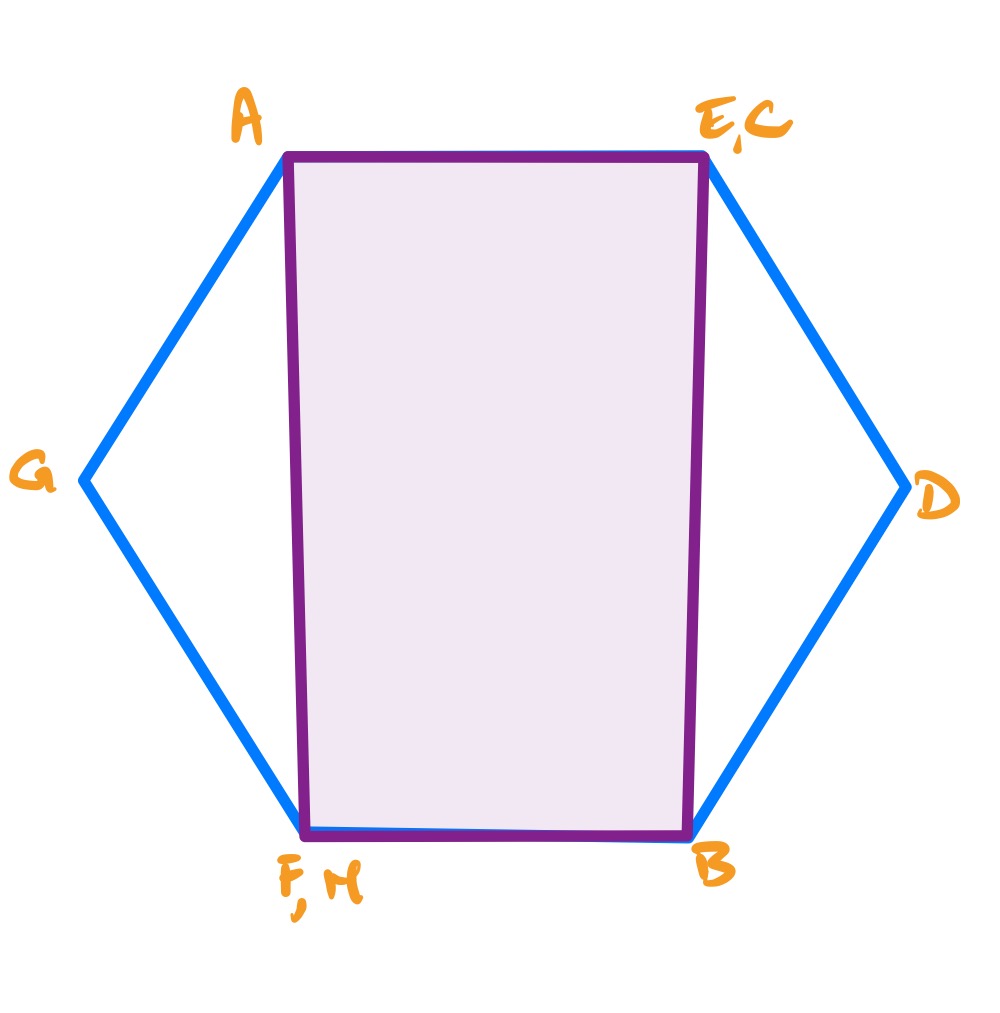
In this second configuration, the left and right hexagons are shrunk to points. This also makes the purple region coincide with a central rectangle, but in a different orientation.