Notes
three quarter circles ii solution
Solution to the Three Quarter Circles II Puzzle
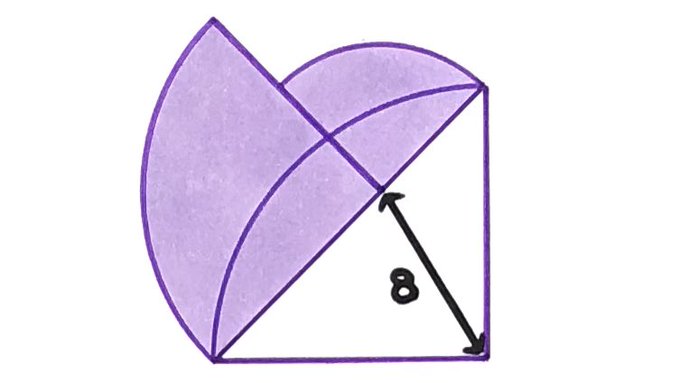
Three quarter circles. What’s the total shaded area?
Solution by Pythagoras' Theorem and Lengths in an Isosceles Right-angled Triangle
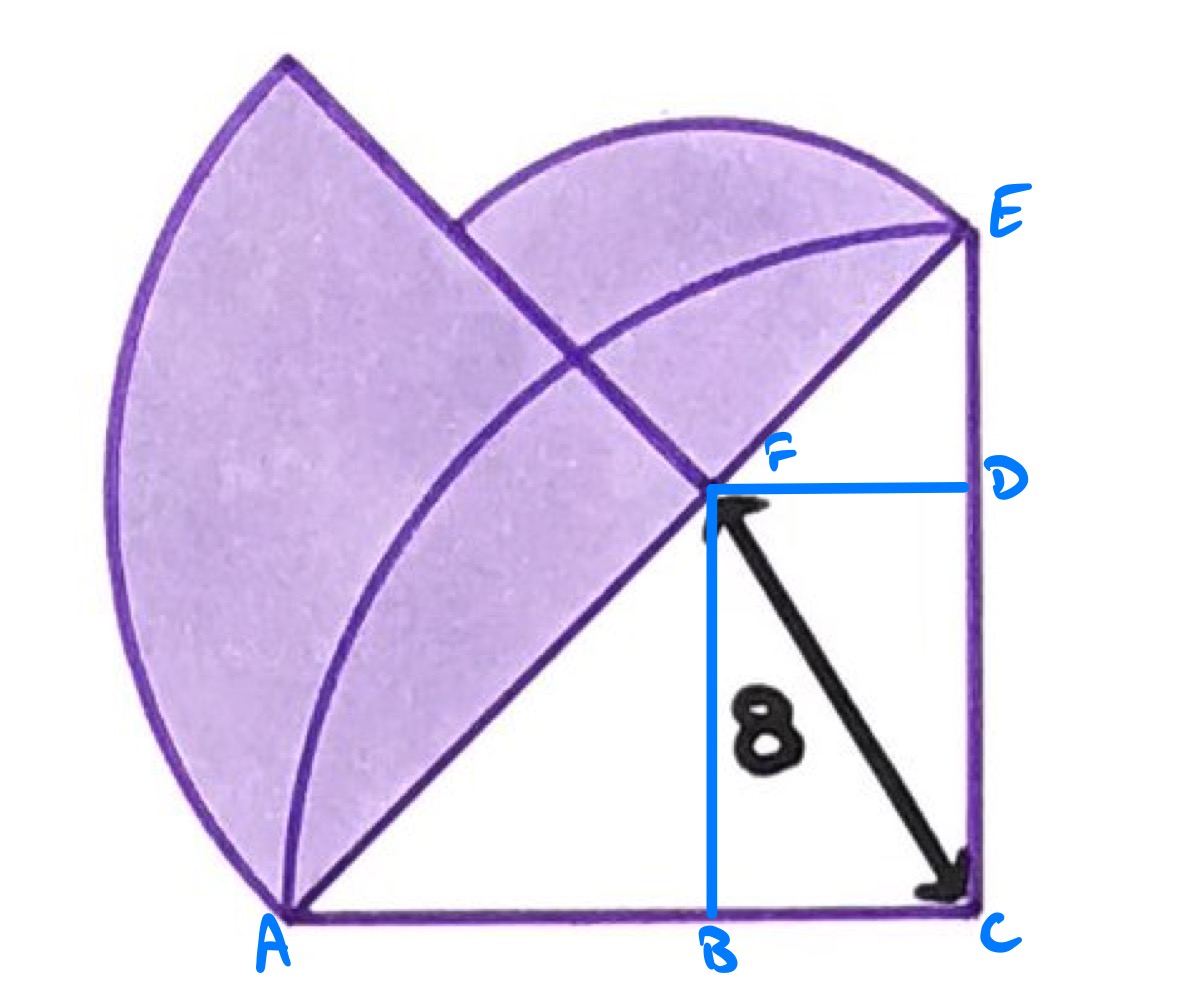
Let the points be labelled as above, where is the point on such that is perpendicular to and on likewise. Let have length and have length . As is a quarter-circle, angle is a right angle, and by construction so are and , so is a rectangle. Therefore also has length . Applying Pythagoras' theorem to triangle we have:
As is a quarter circle, angle is , as is angle . Therefore, triangles and are isosceles right-angled triangles. Hence has length and has length . By the area of a circle, the total shaded area is therefore:
Solution by Invariance Principle
The two shaded quarter circles can be drawn any size relative to each other. There are two special configurations.
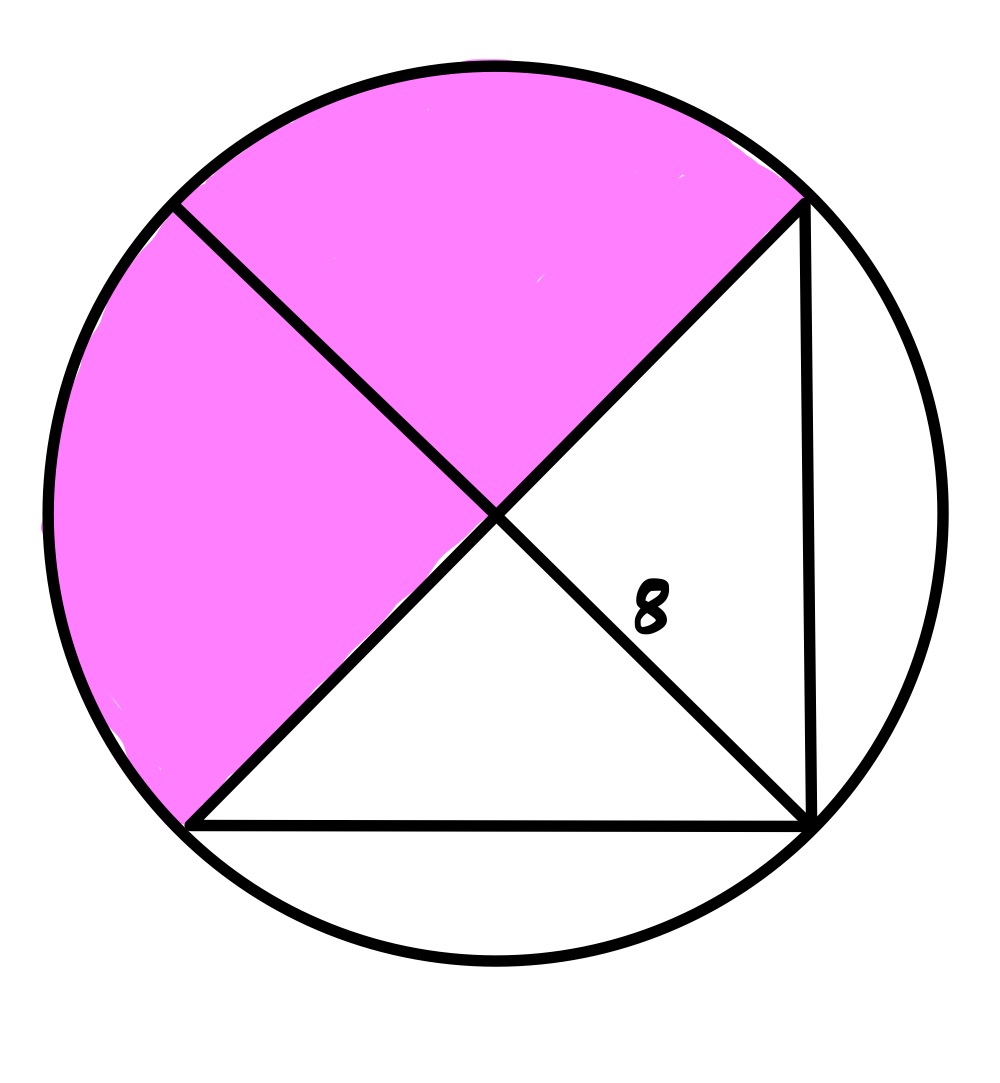
In this configuration, the quarter circles are the same size making a semi-circle. The radius of this semi-circle is , so the area is:
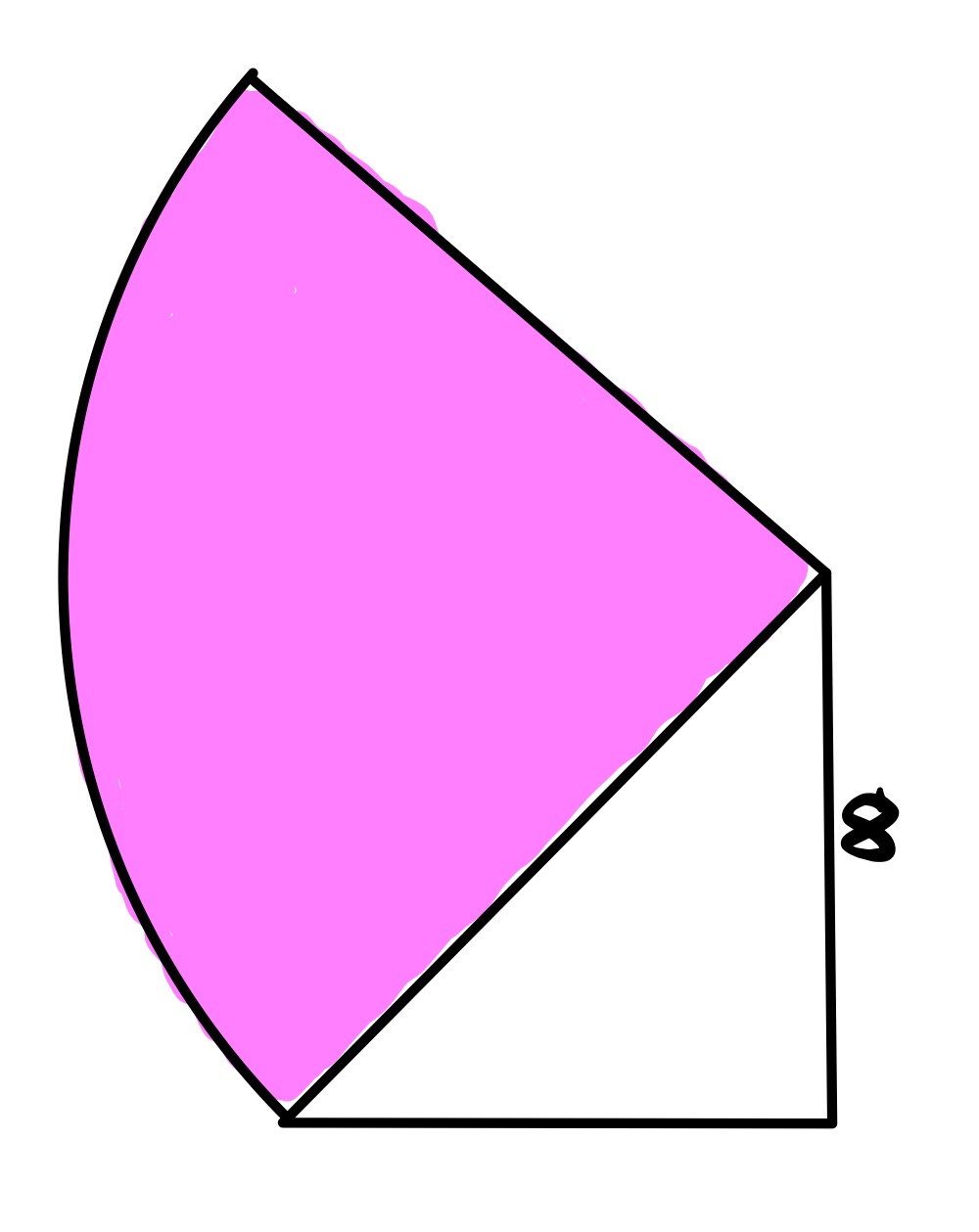
In this version, one quarter circle is shrunk to a point. The radius of the remaining quarter circle is , making its area: