Notes
three congruent rectangles solution
Solution to the Three Congruent Rectangles Puzzle
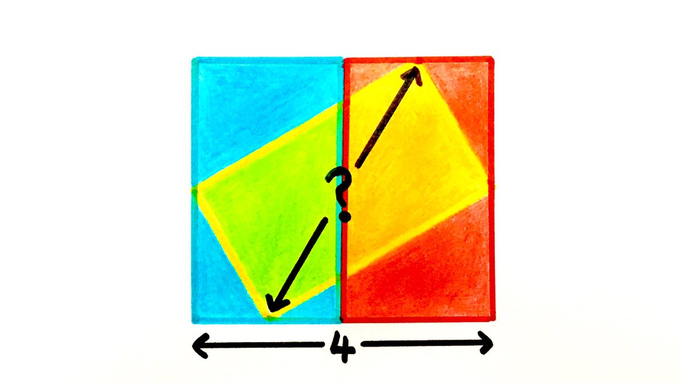
Three congruent rectangles overlap. How long is the diagonal?
Solution by Dissection and Congruent Triangles
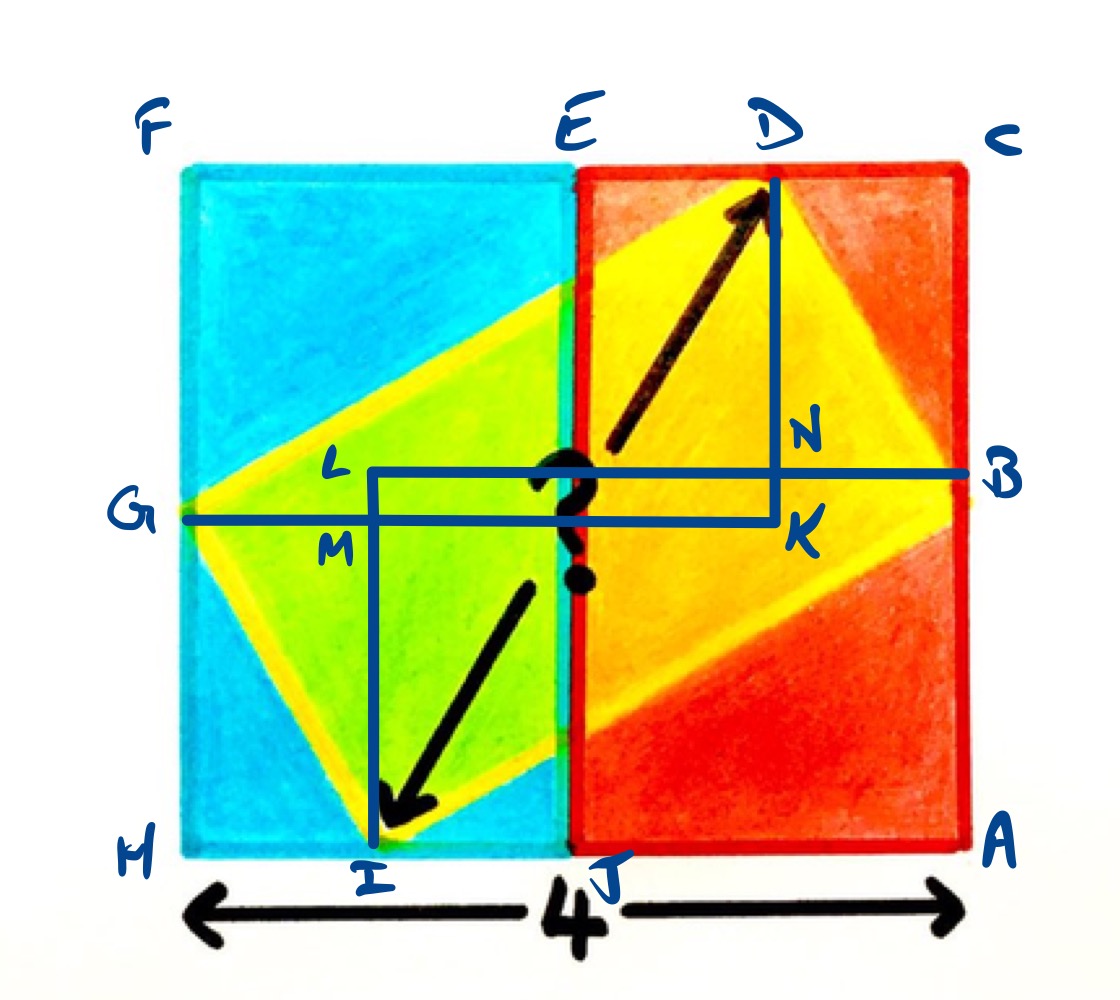
In the above diagram, , , , and are where the the yellow rectangle meets the edges of the figure. Line segments and are horizontal, while and are vertical.
Triangles and are congruent, as are triangle and , triangles and , and triangles and . Therefore the sum of the areas of triangles , , , and is the same as that of triangles , , , and .
The latter comprises the region of the figure that is outside the yellow rectangle, but since the yellow rectangle is congruent to the blue and red, its area is half of the full diagram. Therefore triangles , , , and cover the same area as the yellow rectangle.
But those triangles cover the yellow rectangle with an overlap, namely the rectangle . Therefore, that rectangle must have zero area and so points and are at the same height.
The distance between and is therefore the same as the bottom side of the diagram, which is . This is also the diagonal of the yellow rectangle, so is also the length of line segment .
Solution by Similar Triangles and Pythagoras' Theorem
With the points labelled as above, let line segment have length , have length , and have length . Then has length .
Triangles and are similar since they are both right-angled and angles and add up to . Therefore:
which rearranges to .
Since the rectangles are congruent, has length and has length . Therefore, applying Pythagoras' theorem to triangles and produces:
Putting those together:
Therefore which rearranges to and this has solutions and . Note that is the other solution, so without loss of generality take .
Then , so and likewise . This means that , so the rectangles have side lengths and . Their diagonal is then .