Notes
subdivided triangle iii solution
Solution to the Subdivided Triangle III Puzzle
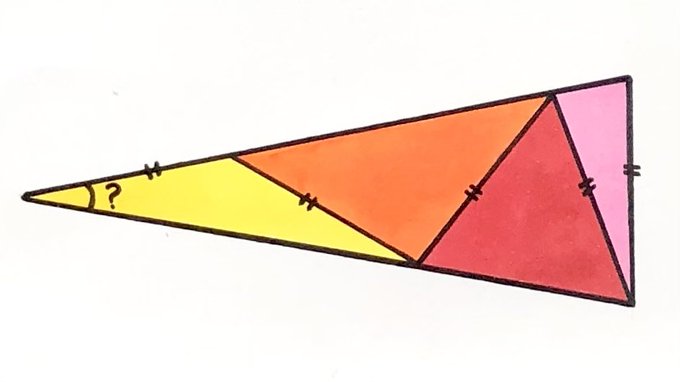
This isosceles triangle has been split into four smaller ones. What’s the missing angle?
Solution by Angles at a Point on a Straight Line, Angles in a Triangle, and Properties of Isosceles Triangles
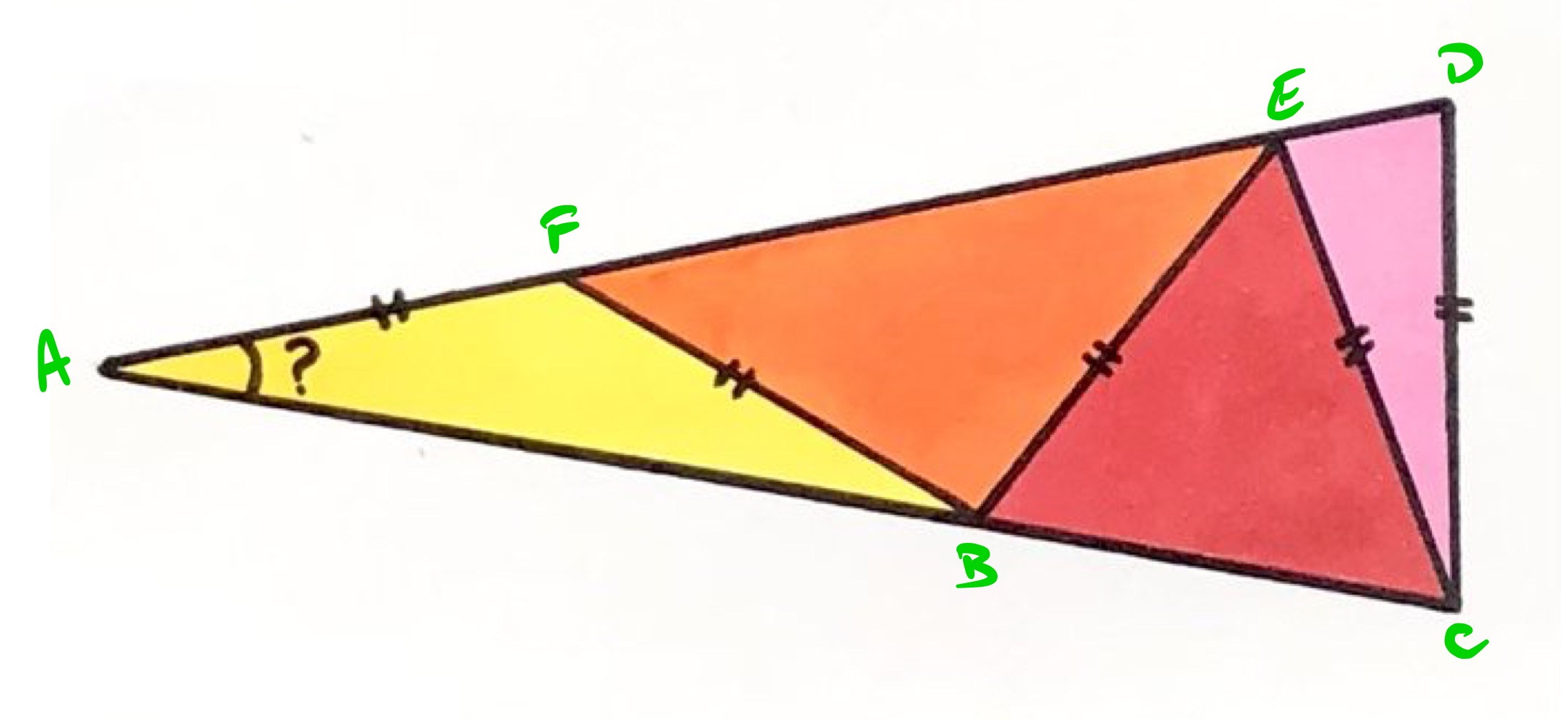
Consider the points labelled as above. Let be the angle at the apex, namely . Then as triangle is isosceles, angles and are both .
Since angles in a triangle add up to , and triangle is isosceles, angle is . Then as angles at a point on a straight line also add up to , angle is .
Then angle is , so as angle is , this leaves angle as . Therefore also angle is .
Triangle is isosceles, and shares angle with triangle , so these triangles are similar, meaning that angle is the same as angle , namely . So angle is .
Therefore,
meaning that .