Notes
subdivided hexagon iv solution
Solution to the Subdivided Hexagon IV Puzzle
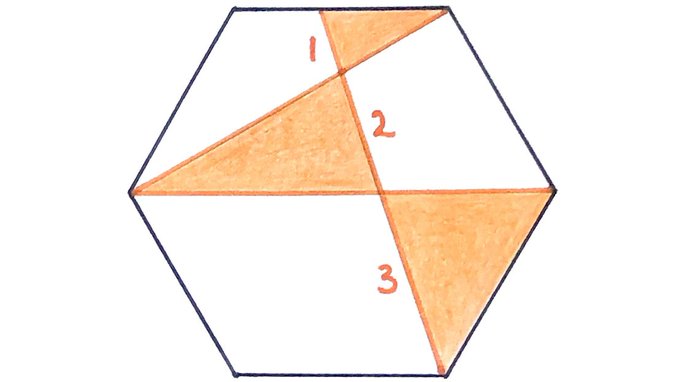
What fraction of this regular hexagon is shaded?
Solution by Area of a Triangle, Properties of a Regular Hexagon, Angles in Parallel Lines, Vertically Opposite Angles, and Similar Triangles
SubdividedHexagonIVLabelled.jpeg?
With the diagram labelled as above, first consider triangle . From the properties of a regular hexagon, this has area one third of the outer hexagon. Triangle has area one twelfth of the outer hexagon, so triangle has area one quarter of the outer hexagon.
Since the lengths of and are in the ratio , so also the areas of triangles and are in the same ratio.
Triangles and are similar because their angles correspond, using angles in parallel lines and vertically opposite angles, and the length scale factor is , so triangle has area four times that of .
Triangles and are also similar also with length scale factor , so area scale factor , while triangles and are congruent, so have the same area. This means that triangle has area twice that of triangle .
Summarising, triangle has area twice that of triangle , so triangle has area three times it. Then triangle has area half of that, so area times that of triangle . Triangle has area four times that of triangle , so the total area of triangle is times that of triangle .
Since this is one quarter of the area of the hexagon, triangle has area one thirtieth of that of the hexagon. As a fraction of the full hexagon, the shaded region therefore has area: