Notes
subdivided hexagon iii solution
Solution to the Subdivided Hexagon III Puzzle
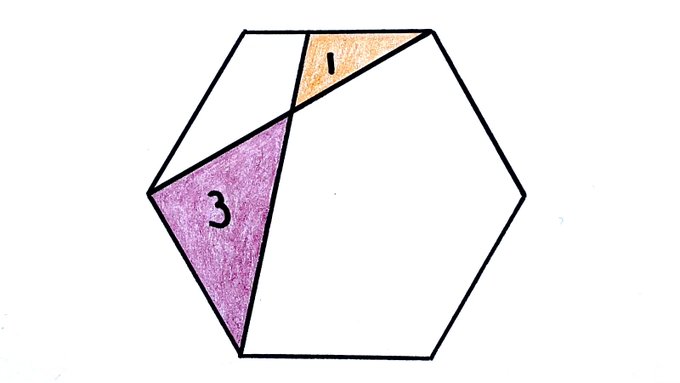
What’s the total area of this regular hexagon?
Solution by Properties of a Regular Hexagon, Similar Triangles, and Solutions of Quadratic Equations
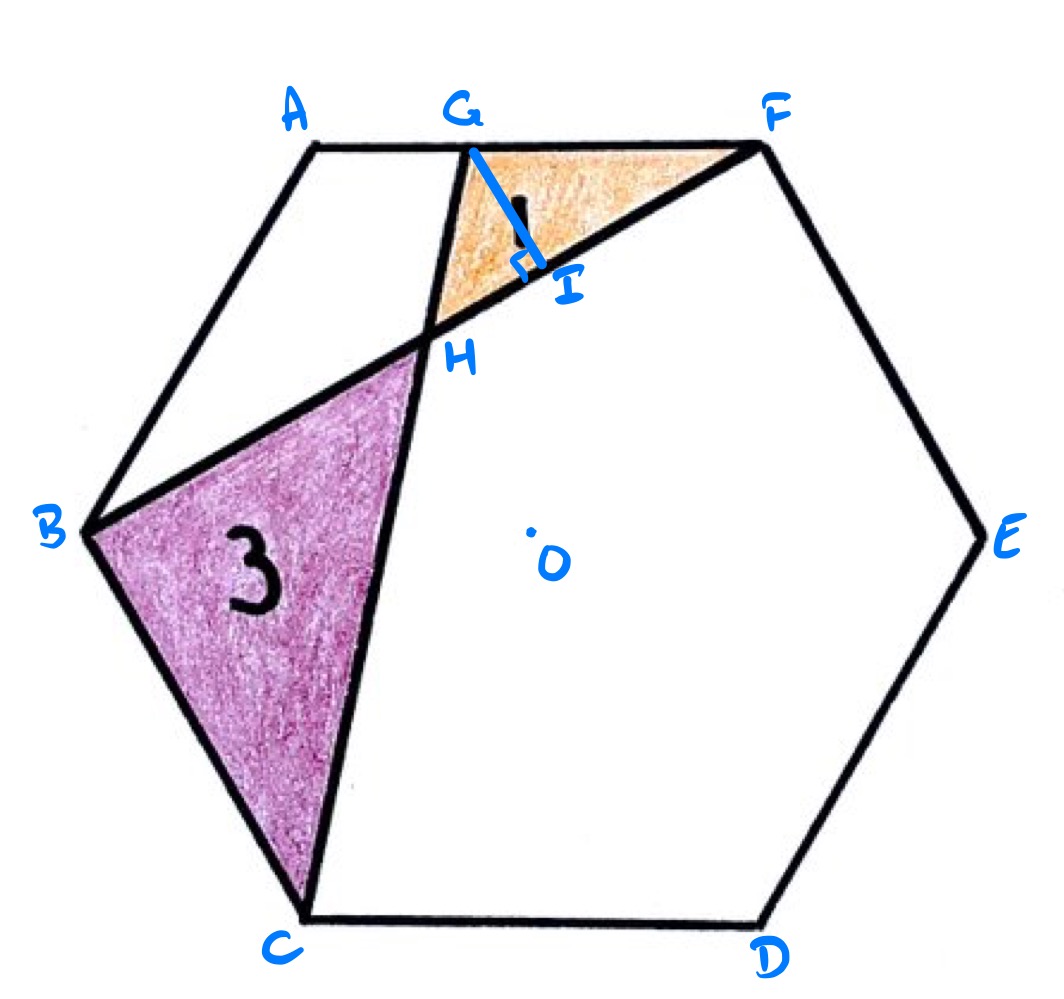
Label the points as in the diagram above, where is such that is perpendicular to .
Let the side length of the hexagon be , then from the area of a regular hexagon, the total area of the hexagon is .
Let line segment have length . Then from the area of the purple triangle, .
Let line segment have length . Using lengths in an equilateral triangle, has length . Triangles and are similar, so line segment has length .
The area of triangle is then , so:
Then, from the lengths in a regular hexagon, line segment has length , so:
This rearranges to:
Putting this into Equation (1) gives:
which rearranges as follows:
Putting turns this into which has solutions and .
From Equation (2), if then , which is negative, so this isn’t a solution to the original problem. Hence and so the area of the hexagon is .
Solution by Equations of Straight Lines, Area of a Triangle, and Properties of a Regular Hexagon
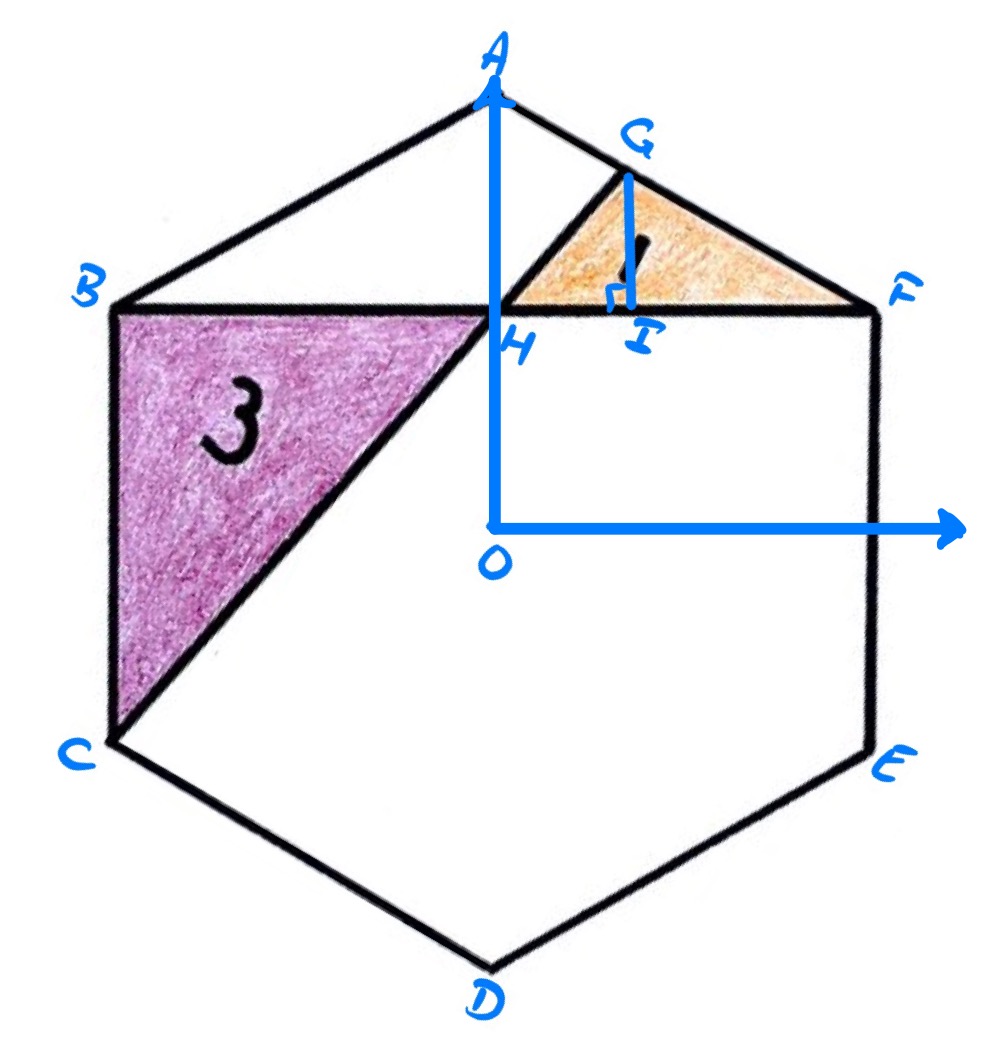
The version of the diagram above is rotated so that is vertically above the centre, . Overlay a coordinate system so that is the origin, is along the vertical axis, and is at the point (note that this is likely to be a different scale than the one that gives the areas).
The point appears to also lie on the vertical axis. This is what will be demonstrated.
In this coordinate system, the line has equation , so has -coordinate . Let its -coordinate be .
Point has coordinates , so the line through and has equation:
Point has coordinates and has coordinates , so the line through and has equation:
This rearranges to .
Point is on the intersection of these lines. Let be its -coordinate, then this satisfies:
which rearranges to:
The areas of the purple and orange triangles are, in this coordinate system, given by and . Since the purple triangle is three times the area of the orange then:
This rearranges as follows:
So either or . The second of these is outside the hexagon, so we must have .
This means that lies on the line , so then the purple triangle is one sixth of the area of the hexagon, meaning that the hexagon has area .