Notes
six squares in a semi-circle and a quarter circle solution

Solution to the Six Squares in a Semi-Circle and a Quarter Circle Puzzle

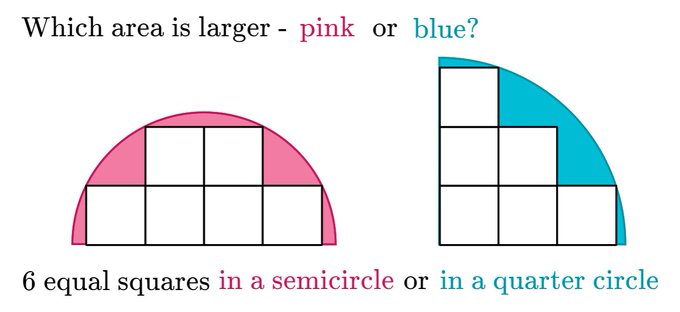
Two Rectangles and a Square II

66 equal squares in a semi-circle and in a quarter circle; which area is larger - pink or blue?

Solution by Pythagoras' Theorem and Area of a Circle

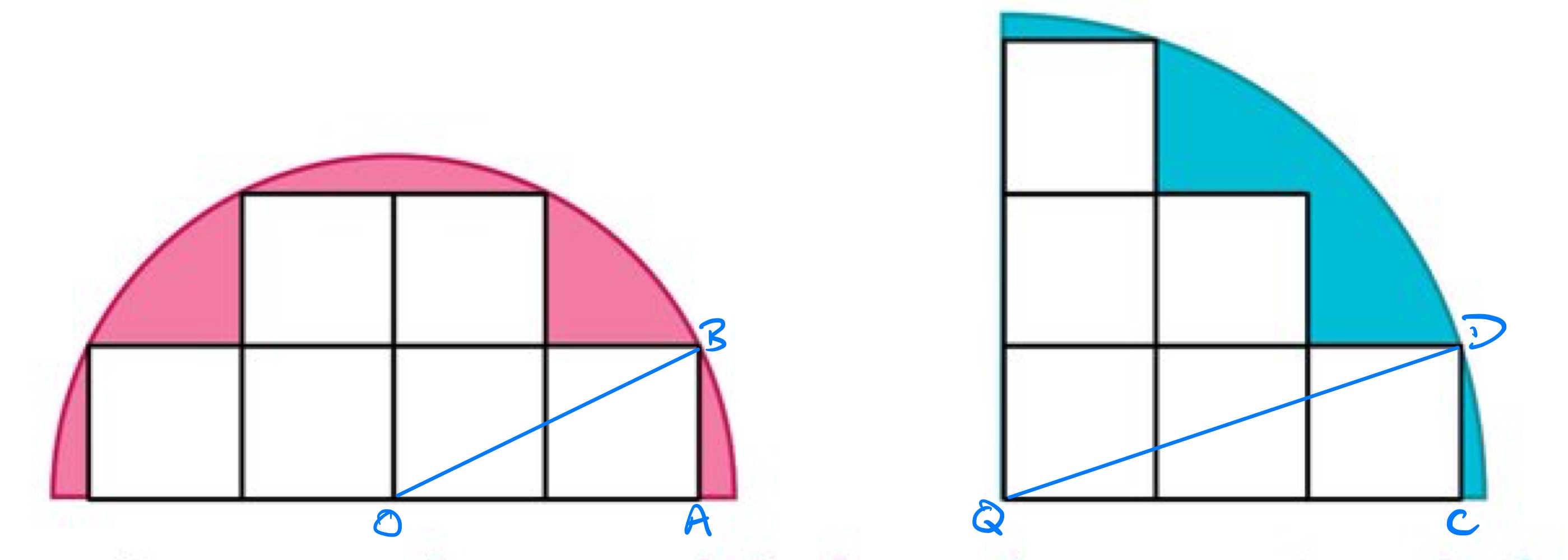
Squares in a semi-circle and quarter circle labelled

Take the side length of the squares as one unit.

Applying Pythagoras' theorem to triangle OABO A B shows that the radius of the pink semi-circle is:

1 2+2 2=5 \sqrt{1^2 + 2^2} = \sqrt{5}

So from the area of a circle, the area of the pink region is:

12π(5) 2−6=52π−6 \frac{1}{2} \pi (\sqrt{5})^2 - 6 = \frac{5}{2} \pi - 6

Applying Pythagoras' theorem to triangle ACDA C D shows that the radius of the blue quarter circle is:

1 2+3 2=10 \sqrt{1^2 + 3^2} = \sqrt{10}

So the area of the blue region is:

14π(10) 2−6=52π−6 \frac{1}{4} \pi (\sqrt{10})^2 - 6 = \frac{5}{2} \pi - 6

Therefore, the pink and blue regions have the same area.

Created on November 1, 2025 19:20:23 by Andrew Stacey?