Notes
rectangles in concentric rings solution

Solution to the Rectangles in Concentric Rings Puzzle

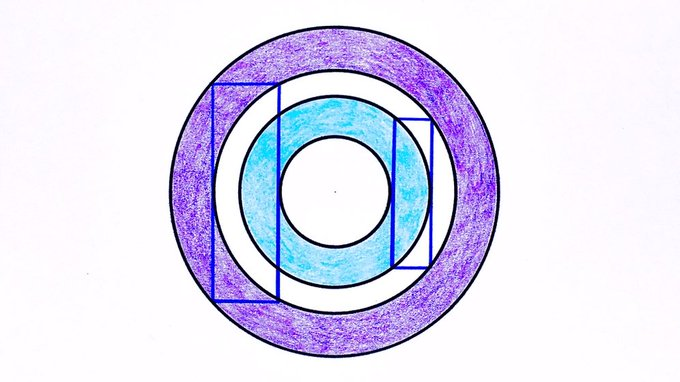
Rectangles in Concentric Rings

Each rectangle is tangent to two of the concentric circles. If the inner blue right has area 44, what’s the purple area?

Solution by Angle Between a Radius and Tangent and Pythagoras' Theorem

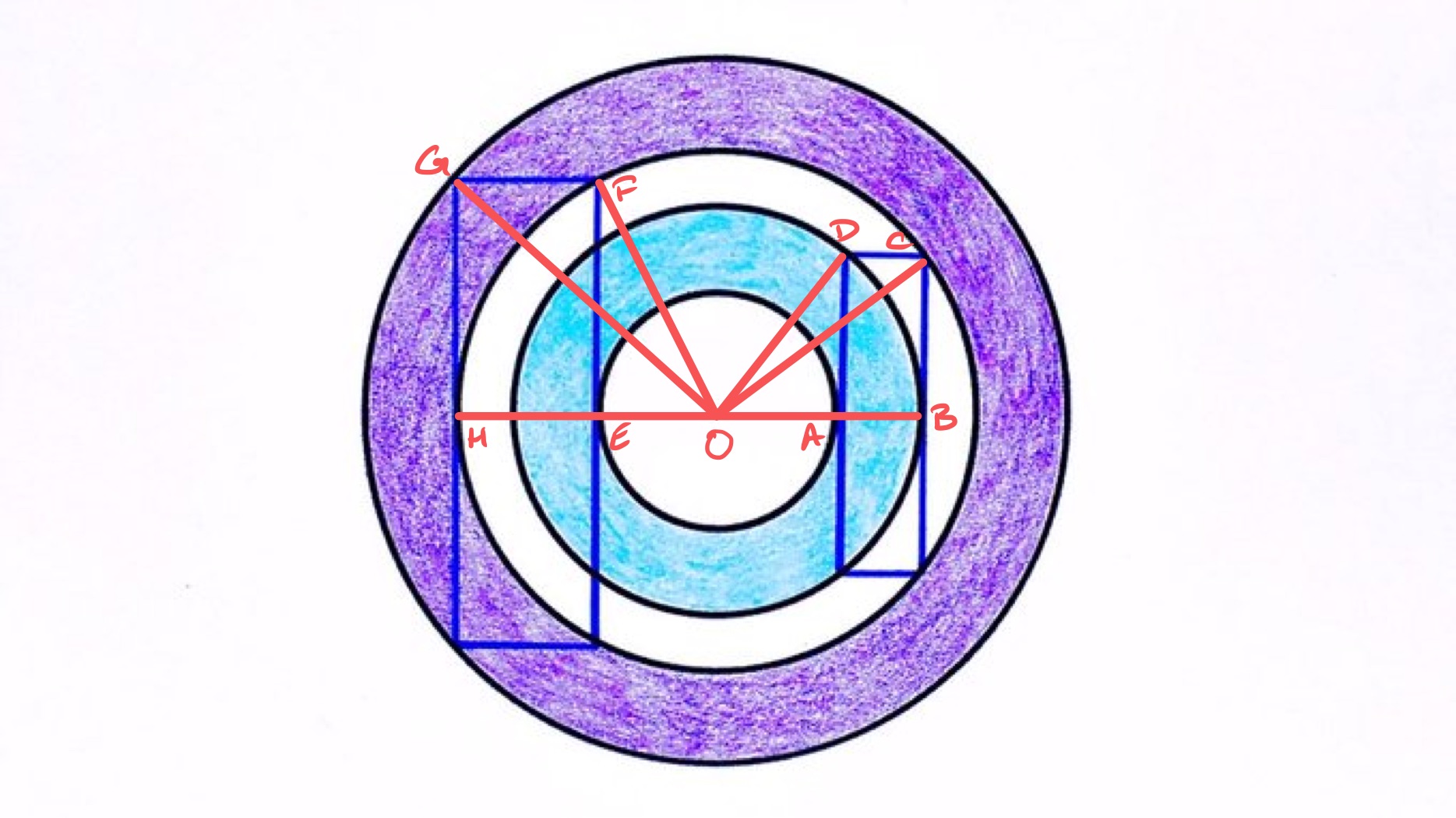
Rectangles in concentric rings labelled

Let aa, bb, cc, dd be the radii of the circles in increasing order. That the blue ring has area 44 means that πb 2−πa 2=4\pi b^2 - \pi a^2 = 4. Let ee and ff be the half heights of the two rectangles, with ee the length of ADA D and ff the length of EFE F.

Using the fact that the angle between a radius and tangent is 90 ∘90^\circ, there are many right-angled triangles in the diagram. Applying Pythagoras' theorem to these triangles leads to the identities:

b 2 =a 2+e 2 ▵OAD c 2 =b 2+e 2 ▵OBC c 2 =a 2+f 2 ▵OEF d 2 =c 2+f 2 ▵OHG \begin{aligned} b^2 &= a^2 + e^2 && \triangle O A D \\ c^2 &= b^2 + e^2 && \triangle O B C \\ c^2 &= a^2 + f^2 && \triangle O E F \\ d^2 &= c^2 + f^2 && \triangle O H G \end{aligned}

The purple ring has area πd 2−πc 2 \pi d^2 - \pi c^2, and using the above identities gives:

d 2−c 2 =f 2 =c 2−a 2 =b 2+e 2−a 2 =b 2+b 2−a 2−a 2 =2(b 2−a 2) \begin{aligned} d^2 - c^2 &= f^2 \\ &= c^2 - a^2 \\ &= b^2 + e^2 - a^2 \\ &= b^2 + b^2 - a^2 - a^2 \\ &= 2(b^2 - a^2) \end{aligned}

Putting this together shows that the purple ring has twice the area of the blue, so has area 88.

Created on August 22, 2021 18:31:47 by Andrew Stacey?