Notes
four squares ix solution
Solution to the Four Squares IX Puzzle
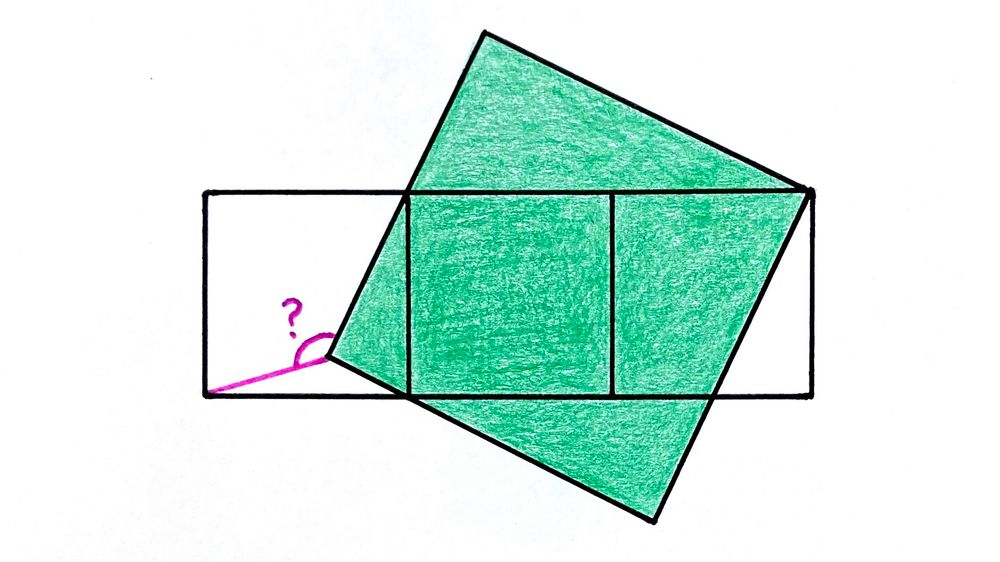
Four Squares. What’s the angle?
Solution by Similar Triangles and Properties of Isosceles Right-angled Triangles
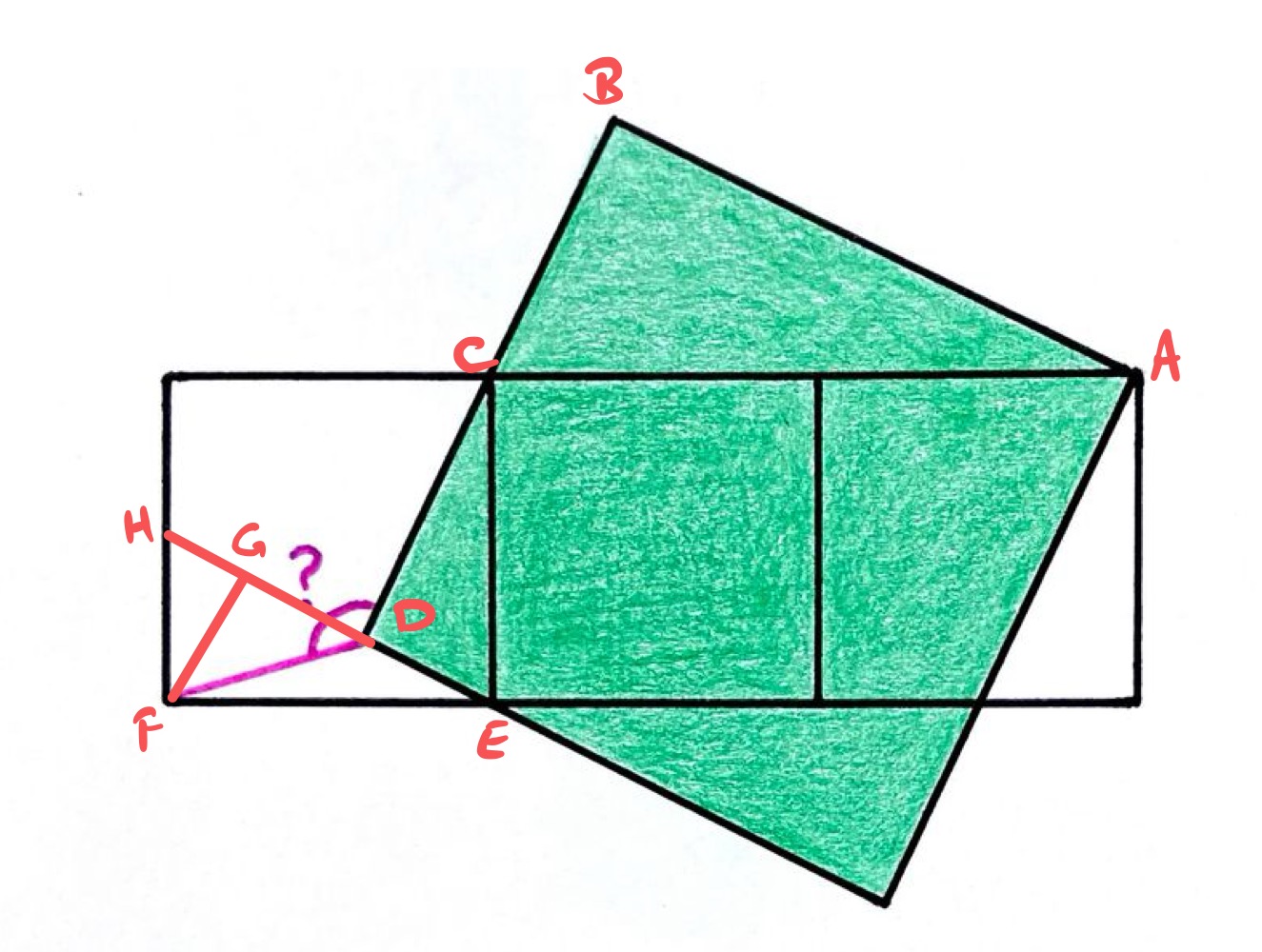
In the above diagram, line segment is the continuation of , and is such that angle is .
Angles , , and add up to since they are angles at a point on a straight line, therefore angles and add up to , since angle is . Then also angles and add up to since is a right-angled triangle. Hence angles and are the same, so triangles and are similar.
Since line segment has twice the length as , so also has twice the length of . But then since has the same length as , this means that also has twice the length of .
Angles and add up to , so triangles and are likewise similar, but then as line segments and are sides of the same square, they have the same length. So in fact, triangles and are congruent.
This means that line segment has twice the length of both line segments and . Therefore, line segments and have the same length, so triangle is an isosceles right-angled triangle.
Therefore, angle is , so angle is .