Notes
four rectangles and a hexagon solution
Solution to the Four Rectangles and a Hexagon Puzzle

What’s the angle hidden inside this trophy made of four squares and a regular hexagon?
Solution by Cosine Rule, Pythagoras' Theorem, and Lengths in a Regular Hexagon
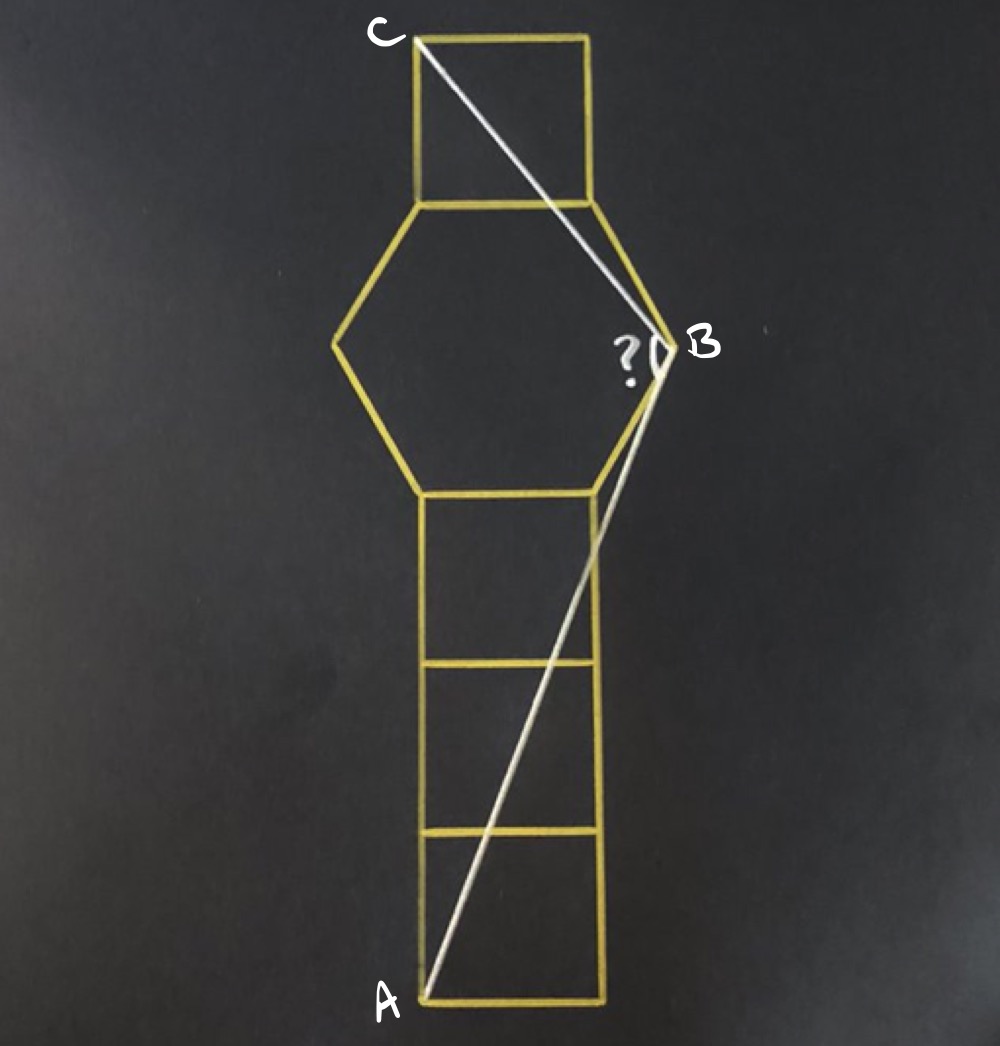
With the side length of the squares as unit, and using the lengths in a regular hexagon and Pythagoras' theorem, the lengths of the sides in triangle are:
- has length
- has length
- has length
Applying the cosine rule, with as the unknown angle, shows:
This means that .
Solution by Lengths in a Regular Hexagon, Angles in a Triangle, and Angles at a Point on a Straight Line
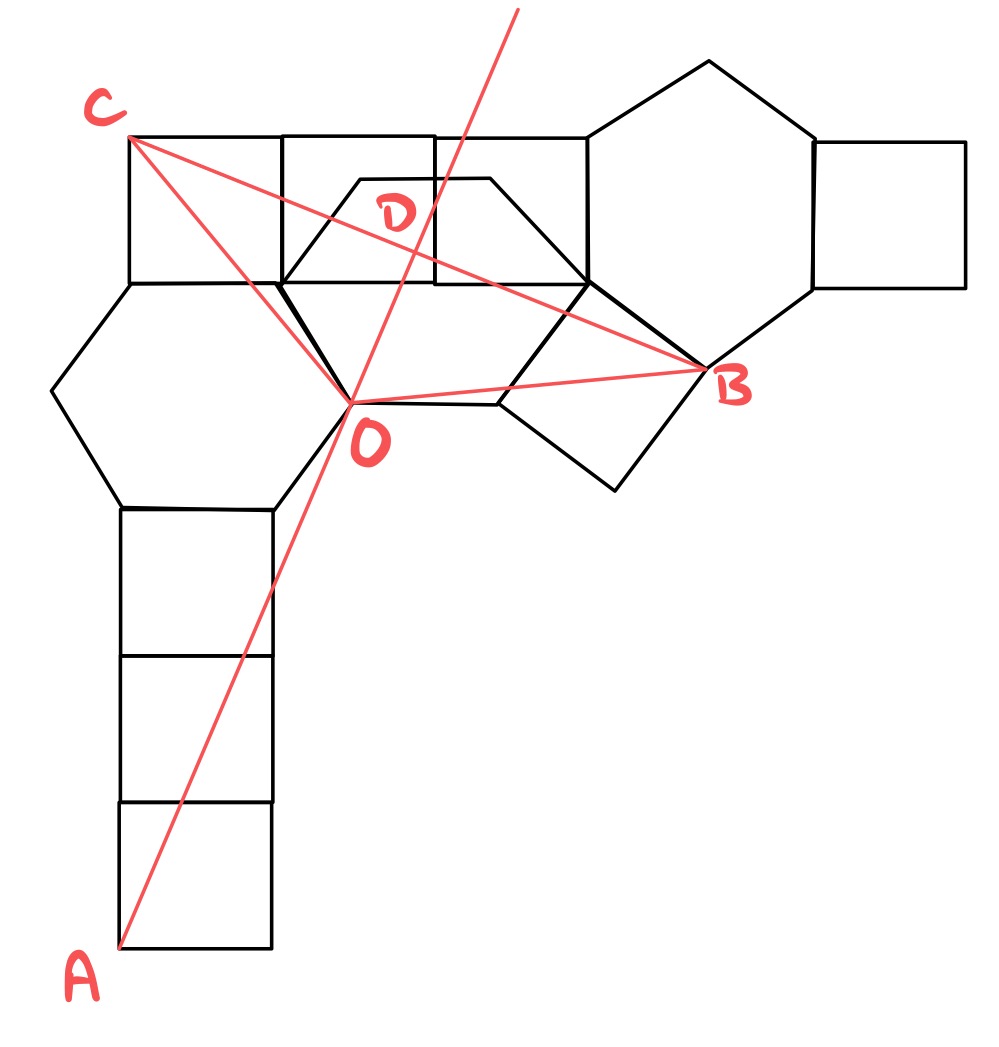
In the above diagram, the original four squares and hexagon are repeated horizontally across the top. Then an additional hexagon and square are included. Since the diameter of a regular hexagon is twice its side length, the extra hexagon spans the two squares and shares a vertex with the horizontal hexagon. This means that the extra square aligns with both hexagons, as shown.
The extra hexagon and square can also be regarded as the top of the original design rotated by about point . This means that line segment has the same length as , and angle is . Then triangle is isosceles so angle is , since angles in a triangle add up to .
Line segment is perpendicular to , so angle is . This means that angle is , and so angle is since angles at a point on a straight line add up to .