Notes
five regular polygons solution
Solution to the Five Regular Polygons Puzzle
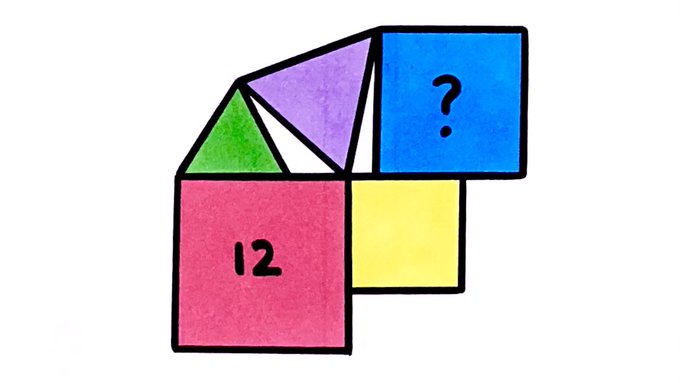
All five polygons are regular. The red square has area 12. What’s the area of the blue square?
Solution by Congruent Triangles and Lengths and Angles in an Equilateral Triangle
FiveRegularPolygonsAnnotated.jpeg?
In the labelled diagram above, is the continuation of so that is an equilateral triangle and is a point on the side of the blue square so that angle is .
Since and have the same length, as do and , it must be that and have the same length. Then angle is the exterior angle of an equilateral triangle so is . Therefore, angles and add up to as the angles in a triangle add up to . So also angles and add up to as angles at a point on a straight line also add up to . Hence angles and are equal. Since and have the same length, and so do and , it is therefore the case that triangles and are congruent.
This means that angle is the same as angle which is , so angles and add up to which means that is parallel to . This means that is a straight line. Since angle is , and angle is by definition of , triangle is equilateral and congruent to triangle .
The length of is the height of above , which is times the length of , and this is the length of . So the length scale factor from the red square to the blue is and therefore the area scale factor is , making the area of the blue square .
Solution by Invariance Principle
The green triangle can vary in size, giving two special configurations.
FiveRegularPolygonsInvarianceA.png?
In this configuration, the purple triangle is perpendicular to the green, meaning that the green triangle with the white space makes half an equilateral triangle. The side length of the purple triangle is therefore times the side length of the red square, and so the blue square has area that of the red square.
FiveRegularPolygonsInvarianceB.png?
In this configuration, the green triangle has the same side length as the red square, as does the purple triangle. The blue square then has side length the height of the purple triangle, being times that of the red square. This leads to an area of as before.