Notes
five rectangles in a semi-circle solution

Solution to the Five Rectangles in a Semi-Circle Puzzle

Solution by Pythagoras' Theorem and the Perpendicular Bisector of a Chord

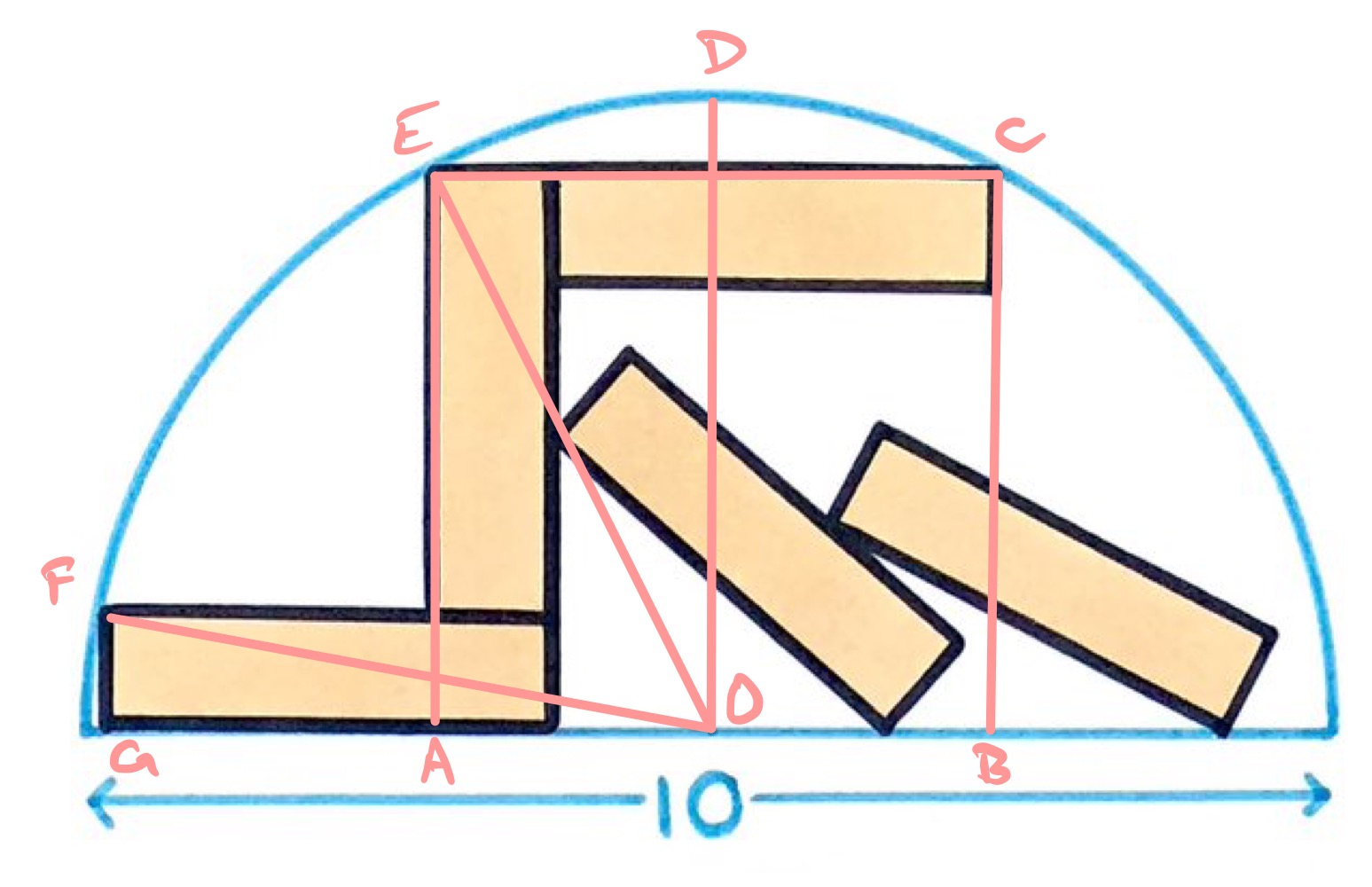
With the points labelled as above, $O$ is the centre of the semi-circle, which has radius $5$.

Let the sides of the rectangles be $a$ and $b$, with $a \gt b$. Then chord $E C$ has length $a + b$, so since $O D$ bisects? this chord, $O A$ has length $\frac{a + b}{2}$. Applying Pythagoras' theorem to triangle $O A E$ then shows that:

Hence $a^2 + 2 a b + b^2 = (a + b)^2 = 20$.

Then $A G$ has length $a - b$ so $O G$ has length $a - b + \frac{a + b}{2} = \frac{3a - b}{2}$. Applying Pythagoras' theorem to triangle $O G F$ shows that:

Hence $9a^2 - 6 a b + 5 b^2 = 100$.

Subtracting these two equations leads to:

So $a = 4 b$, meaning that the area of one rectangle is $a b = 4 b^2$, and also:

Therefore the area of $5$ rectangles is: