Notes
five equilateral triangles ii solution
Solution to the Five Equilateral Triangles II Puzzle
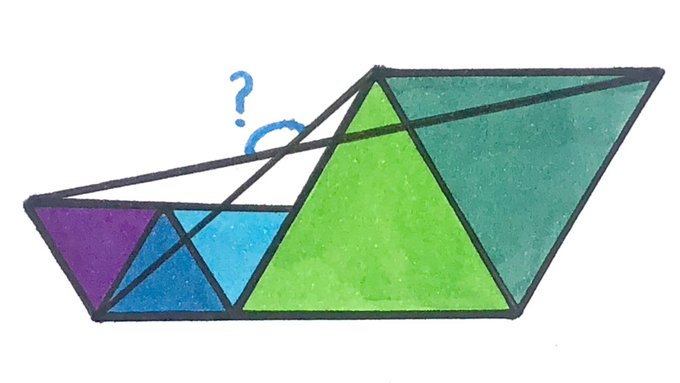
The five triangles are equilateral. What’s the angle?
Solution by Rotation, Angles in Isosceles Triangles, Corresponding Angles, and Angles at a Point on a Straight Line
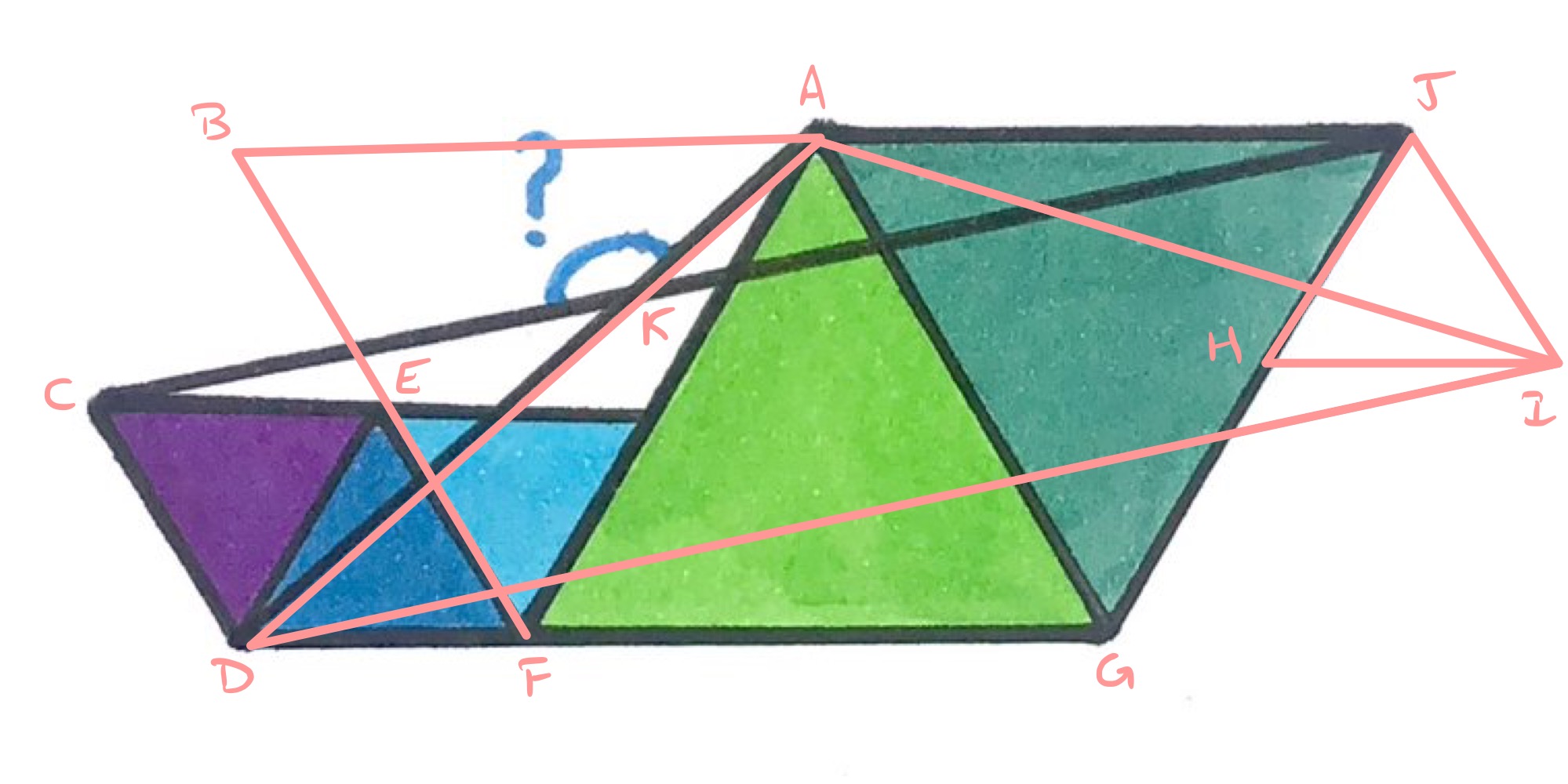
In the above diagram, triangle is another large equilateral triangle and is another small one.
Triangle is obtained from triangle by rotating about . This also takes triangle to triangle . Therefore, line segment is the rotation by of line segment about . Hence angle is and triangle is isosceles. This means that angle is since angles in a triangle add up to .
Finally, line segments and are parallel, so angles and are equal as they are corresponding angles. Then angle since angles at a point on a straight line add up to .
Solution by Invariance Principle
The relative sizes of the equilateral triangles is not specified, and varying this leads to two configurations where the answer is more clear. In both, the lines have to be extended to ensure that the angle is well-defined.
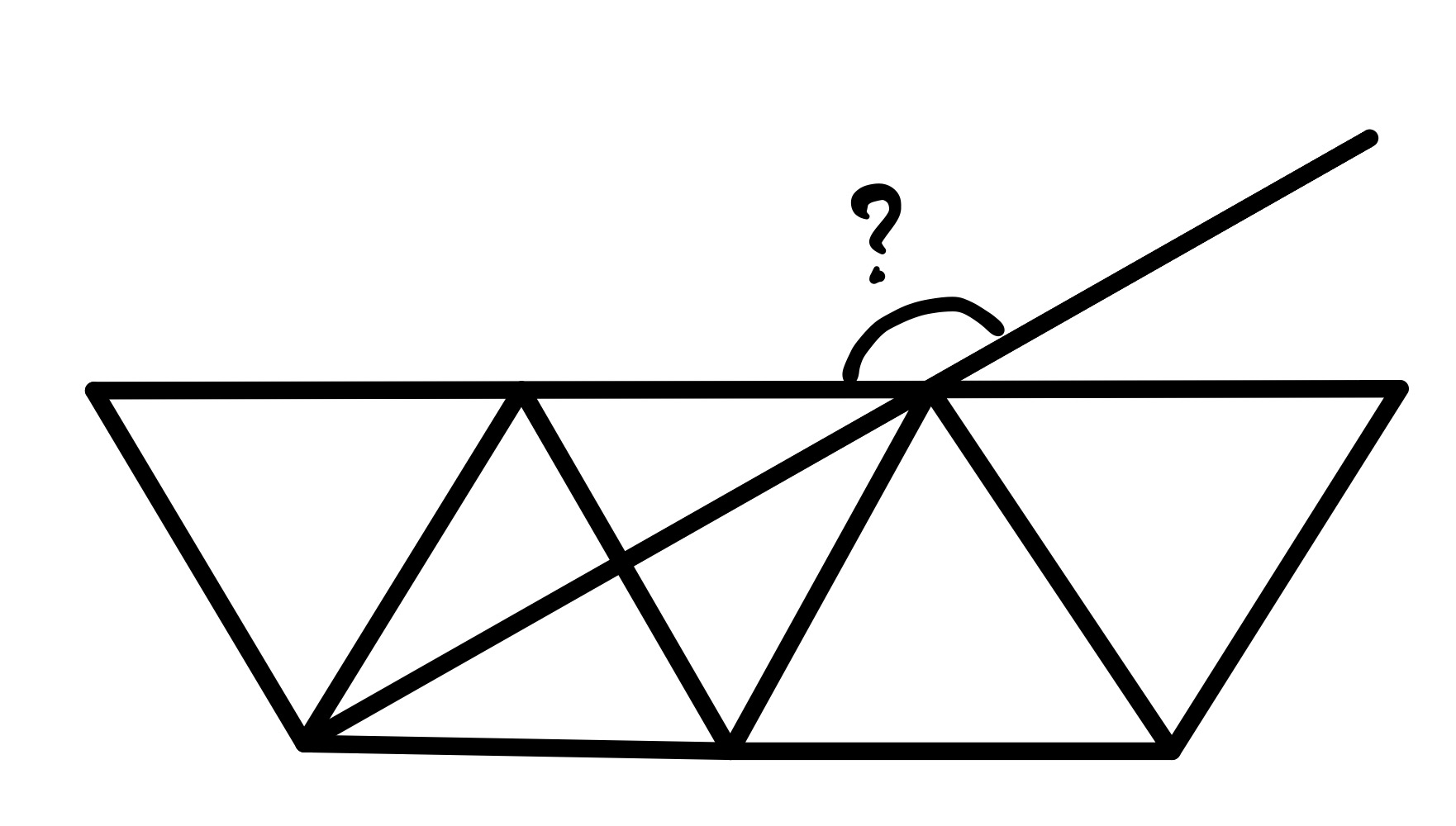
In this configuration, all the equilateral triangles are the same size. The extra line bisects one of the equilateral triangles, meaning that the acute angle is half of and so the requested angle is .
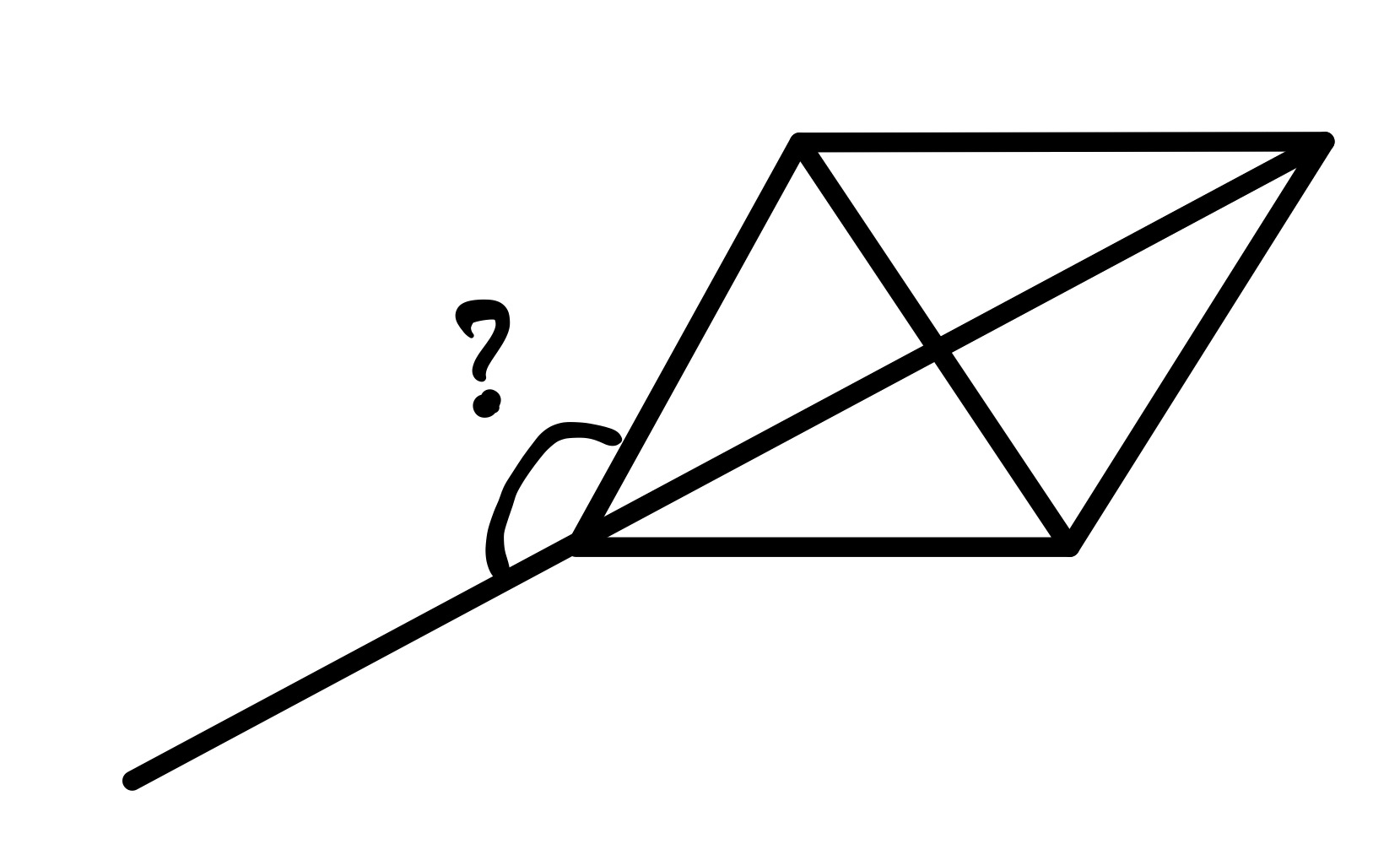
In this configuration, the smaller equilateral triangles have been shrunk down to a point. The requested angle is by a similar argument.