Notes
a quarter circle and a semi-circle in a triangle solution
Solution to the A Quarter Circle and a Semi-Circle in a Triangle Puzzle
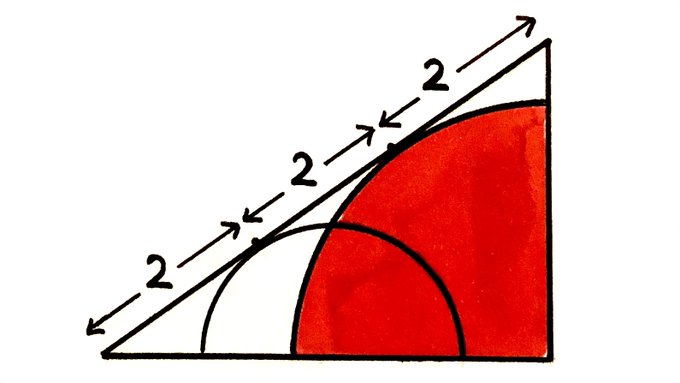
What’s the area of the quarter circle?
Solution by Pythagoras' Theorem and Angle Between a Radius and Tangent
Note: the semi-circle seems redundant in this puzzle
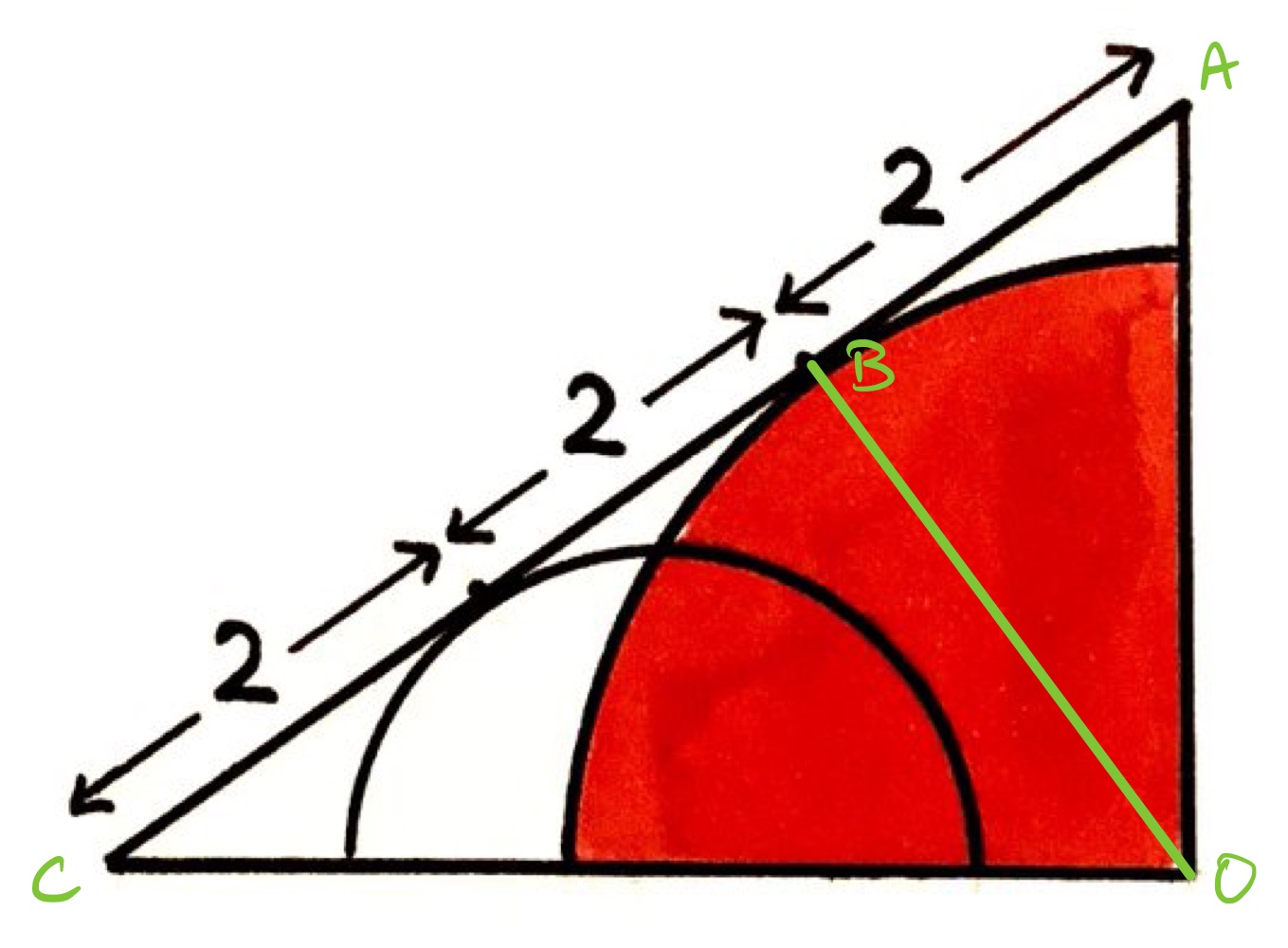
With the points labelled as above, let be the radius of the quarter circle, the length of line segment , and the length of line segment .
Since the red region is a quarter circle, angle is . Therefore the outer triangle is right-angled. Applying Pythagoras' theorem shows that:
As the angle between a radius and tangent is also , triangles and are also right-angled. Applying Pythagoras' theorem to those shows that:
Adding these equations together shows that and so , from which .
Therefore, the area of the quarter circle is:
Solution by Angle Between a Radius and Tangent, Angles in a Triangle, and Similar Triangles
As above, triangles and are right-angled. Angles and add to , but then so also do angles and . So angles and are the same, so triangles and are similar.
Therefore, the ratios and are the same, leading to as before.