Notes
a circle in a rectangle solution
Solution to the A Circle in a Rectangle Puzzle
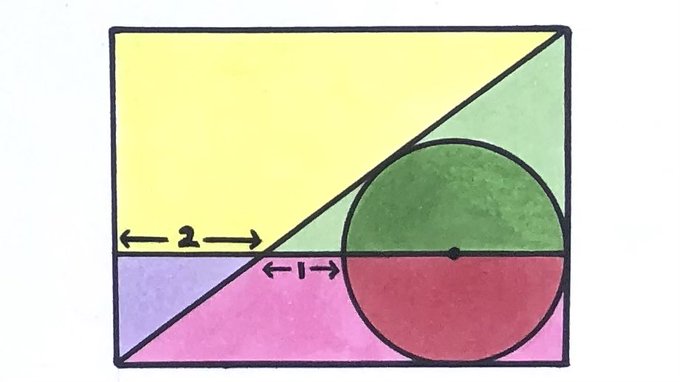
What’s the area of this rectangle?
Solution by Pythagoras' Theorem, Angle Between a Radius and Tangent, Vertically Opposite Angles, and Similar Triangles
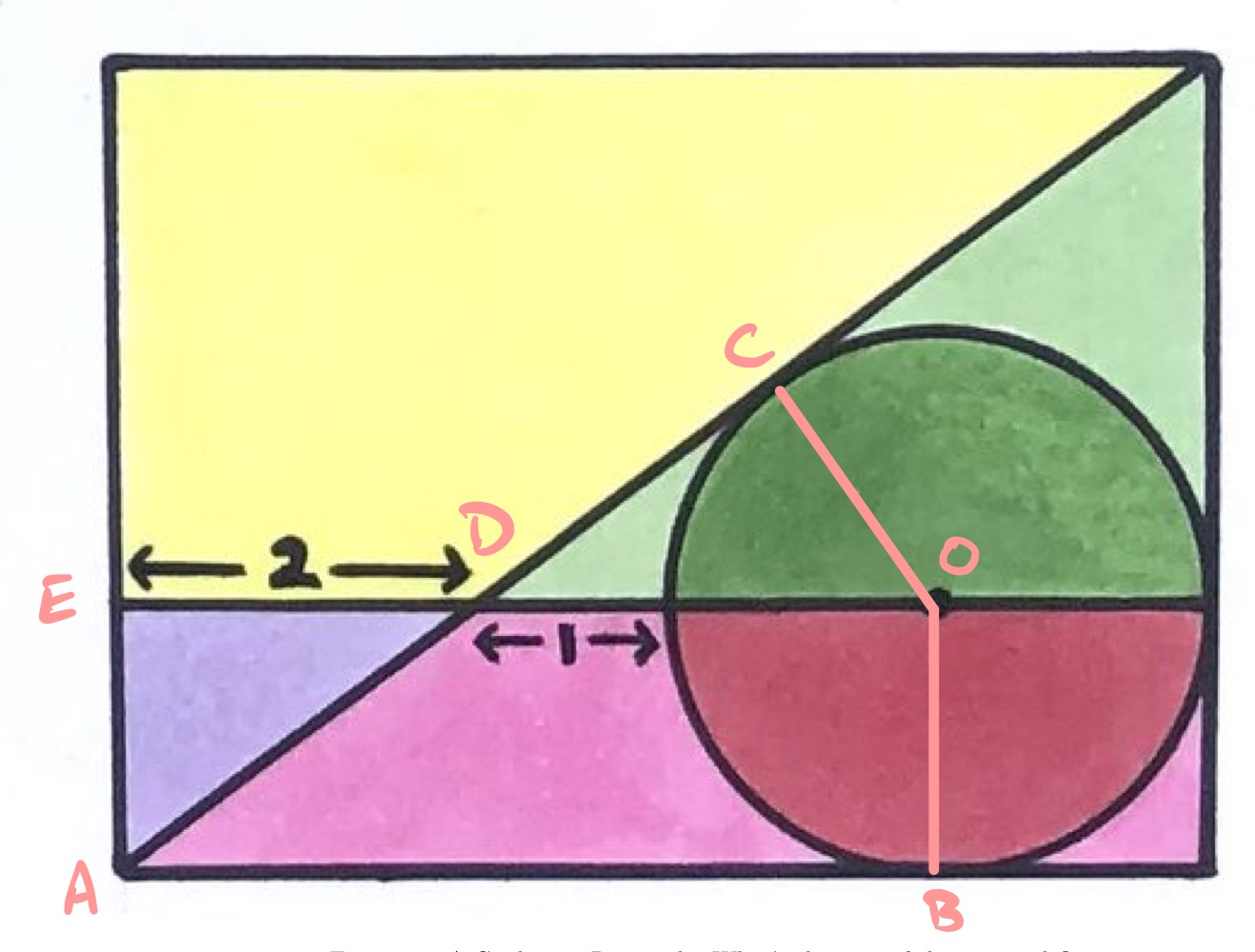
In the diagram above, is the centre of the circle. Let be the radius of the circle.
As the angle between a radius and tangent is , line segments and are vertical and horizontal, respectively. So has length . Since angles and are vertically opposite, they are equal. Then since triangles and are right-angled and and have the same length, they are congruent. Hence has length .
The other sides in triangle have lengths and , so applying Pythagoras' theorem shows that:
This simplifies to which means that .
The width of the rectangle is then . The sides of the rectangle are in the same ratio to the corresponding sides of triangle , so the height of the rectangle is .
The area of the rectangle is therefore .