Created on November 15, 2025 00:17:41 by Andrew Stacey (81.109.65.126).
These are the techniques used in solving the problem two triangles in a semi-circle.
Created on November 15, 2025 00:17:01 by Andrew Stacey (81.109.65.126).

These triangles are congruent and isosceles. What’s the area of the semicircle?
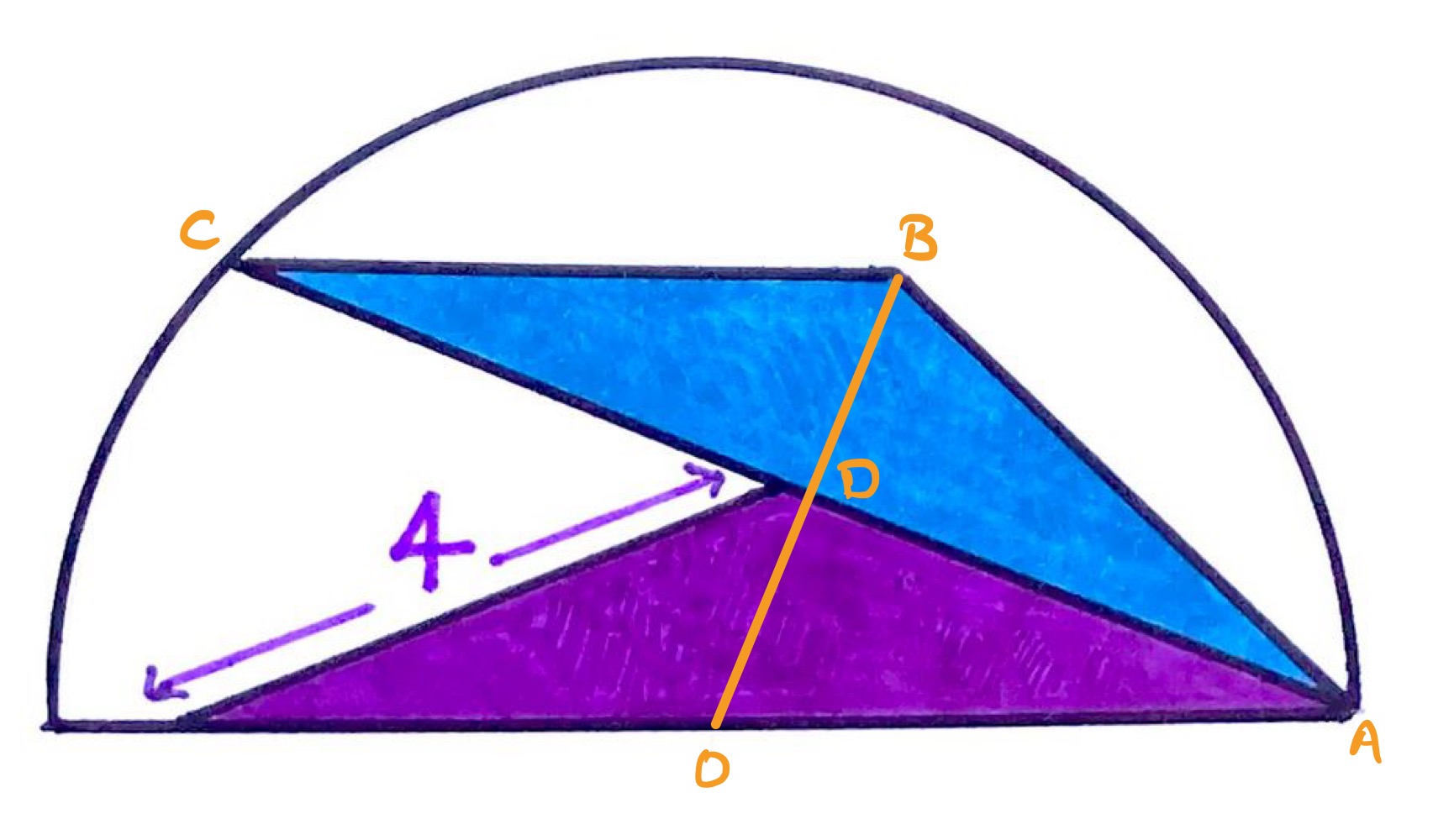
In the diagram above, is the centre of the semi-circle and is the midpoint of chord . As such, the perpendicular bisector of , which passes through , also passes through .
Since is the base of the isosceles triangle , that perpendicular bisector also passes through . So is a straight line.
Triangles and are both right-angled at . Since the blue and purple triangles are congruent, angles and are equal. Therefore, triangles and have the same interior angles and share side so are congruent.
This means that line segments and have the same length. Then since the triangles are congruent and isosceles, has length , so the radius of the semi-circle is also and its area is then:
Created on November 15, 2025 00:02:18 by Andrew Stacey (81.109.65.126).
These are the techniques used in solving the problem three congruent rectangles vi.
Created on November 15, 2025 00:01:35 by Andrew Stacey (81.109.65.126).
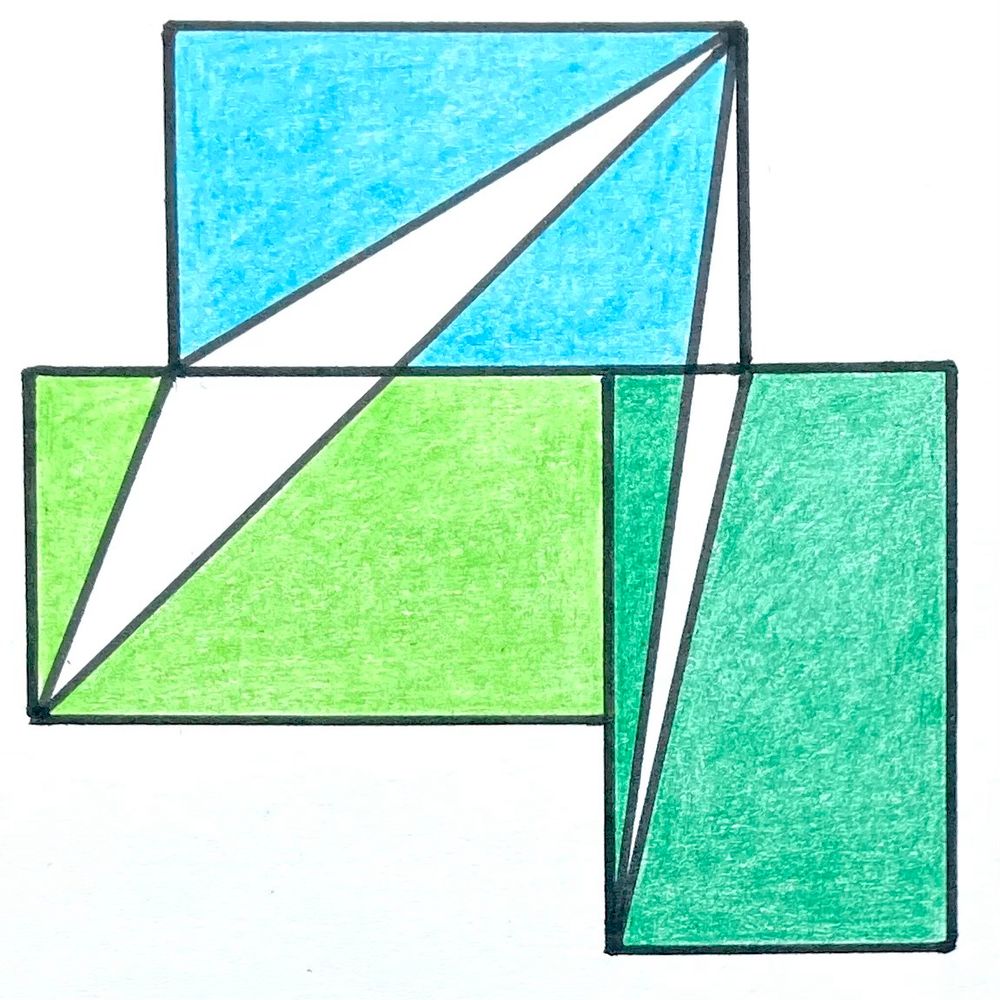
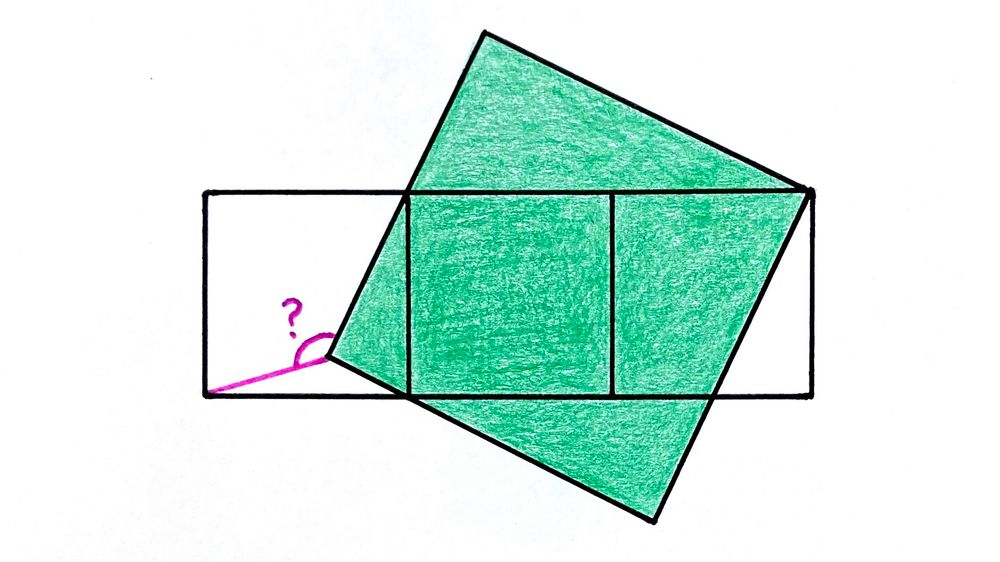
The three rectangles are congruent. What fraction of the design is shaded?
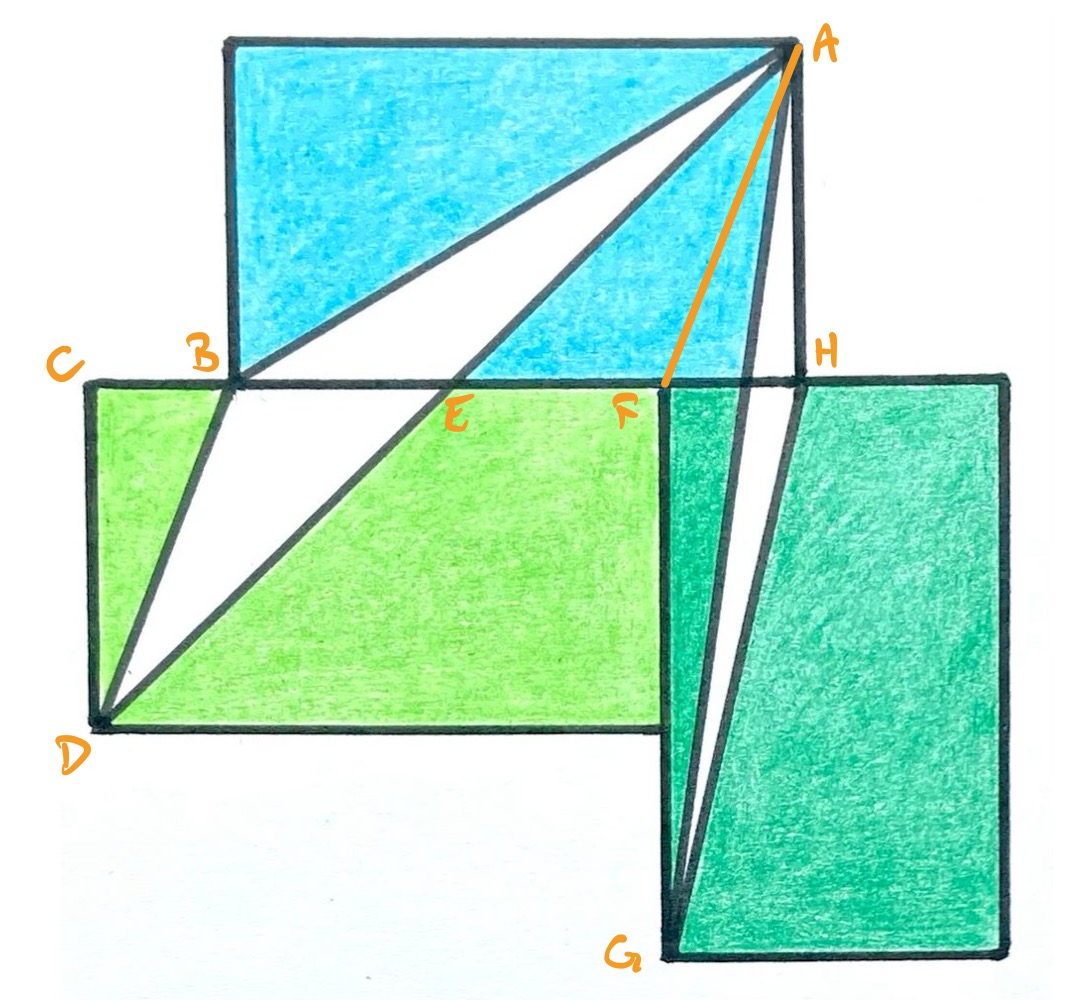
Consider the diagram labelled as above. Triangles and share the base , and as is parallel to , the points and have the same perpendicular distance to , so triangles and have the same area.
Since the rectangles are congruent, line segments and have the same length, so so do and . Therefore is parallel to . Since also and have the same length then triangles and are congruent.
The white regions therefore have the same area as triangle , which comprises one half of one of the rectangles and so one sixth of the design.
Created on November 14, 2025 23:09:44 by Andrew Stacey (81.109.65.126).
These are the techniques used in solving the problem four squares x.
Created on November 14, 2025 23:09:09 by Andrew Stacey (81.109.65.126).
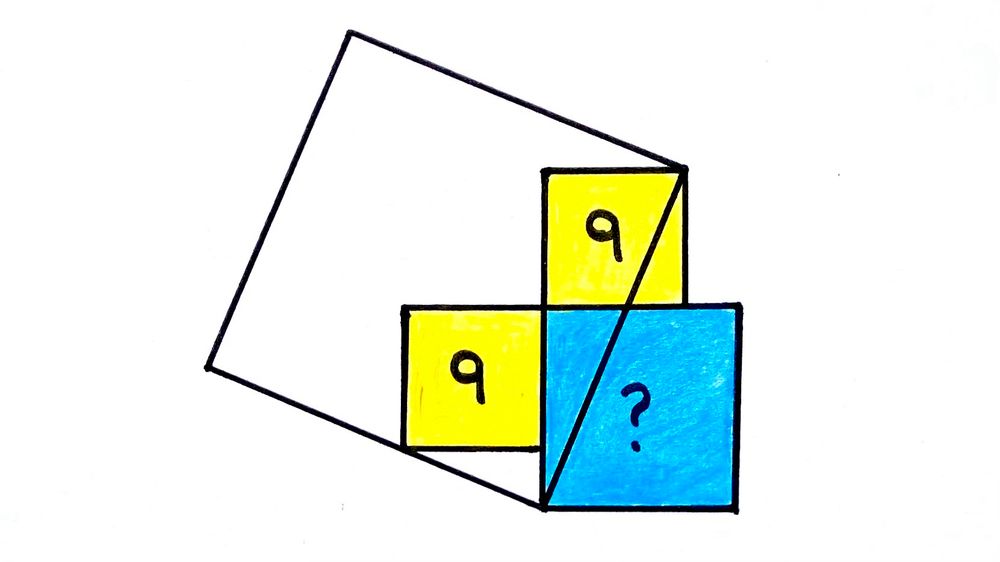
Four squares. What’s the blue square’s area?
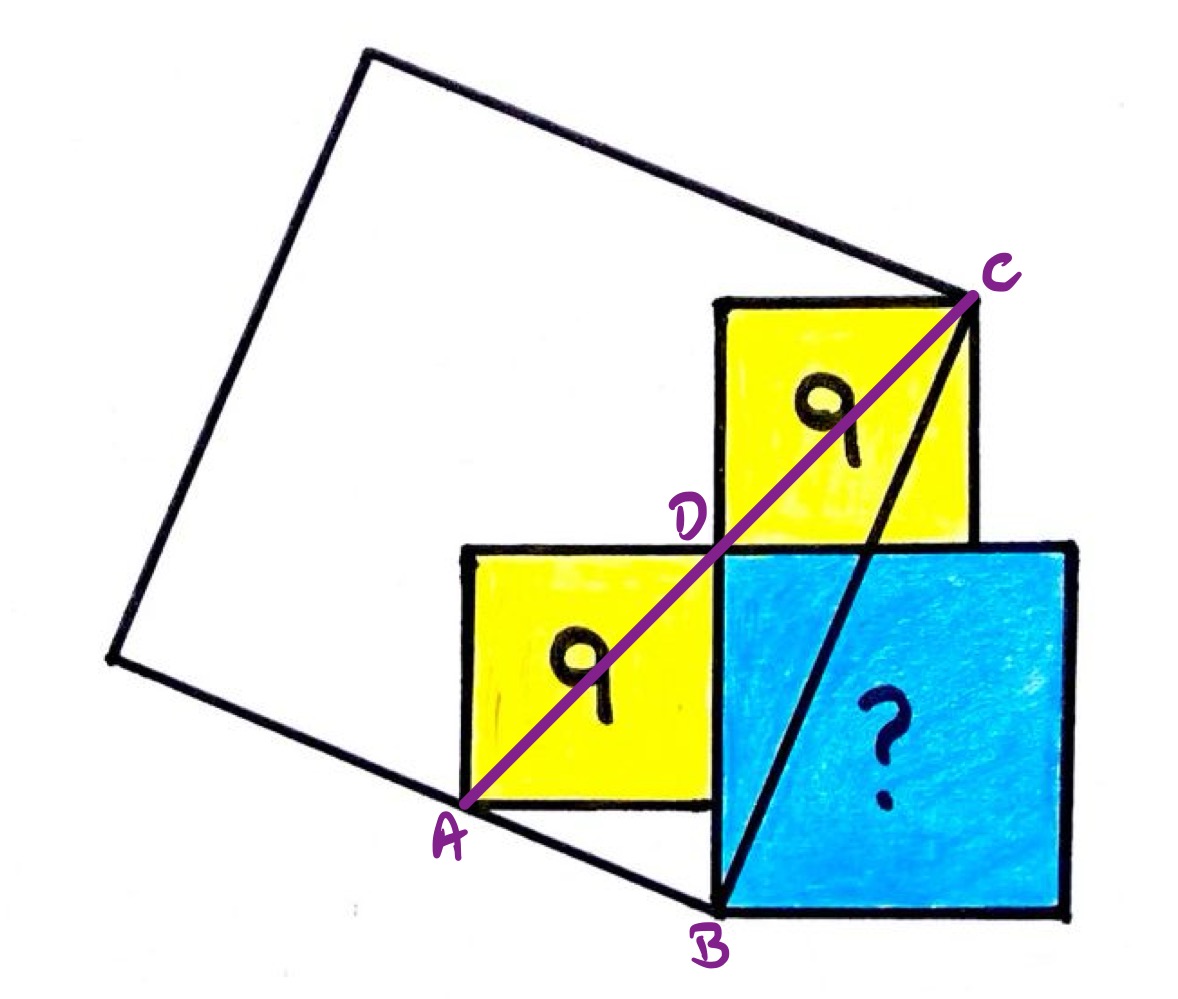
In the diagram labelled as above, is a straight line so triangle is a right-angled triangle with as the midpoint of its hypotenuse. Therefore, by the properties of right-angled triangles, line segment has the same length as . Then from the properties of squares, the blue square has twice the area of each of the yellow squares, so has area .
Created on November 14, 2025 22:20:38 by Andrew Stacey (81.109.65.126).
These are the techniques used in solving the problem four quarter circles iii.
Created on November 14, 2025 22:19:44 by Andrew Stacey (81.109.65.126).
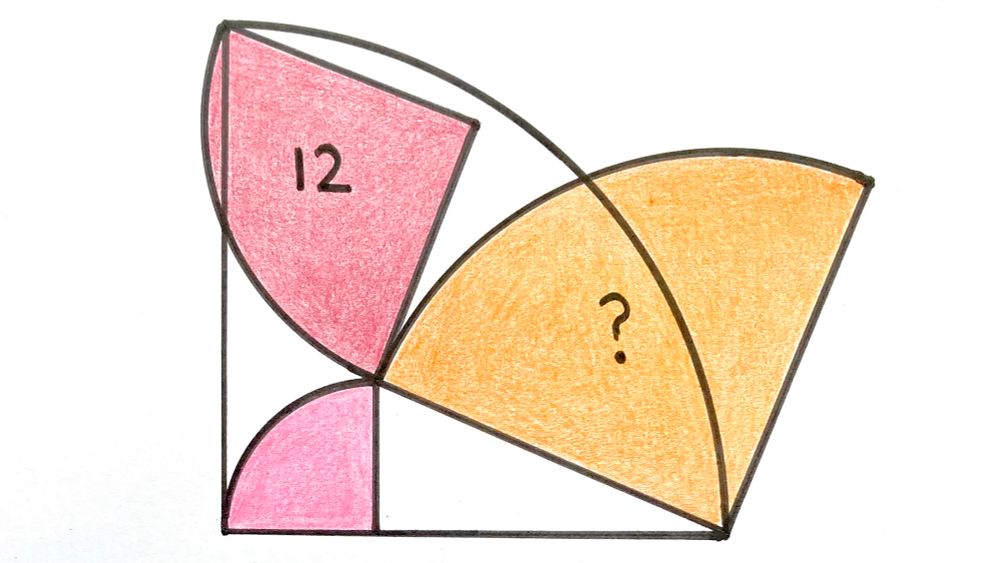
Four quarter circles. What’s the area of the orange one?
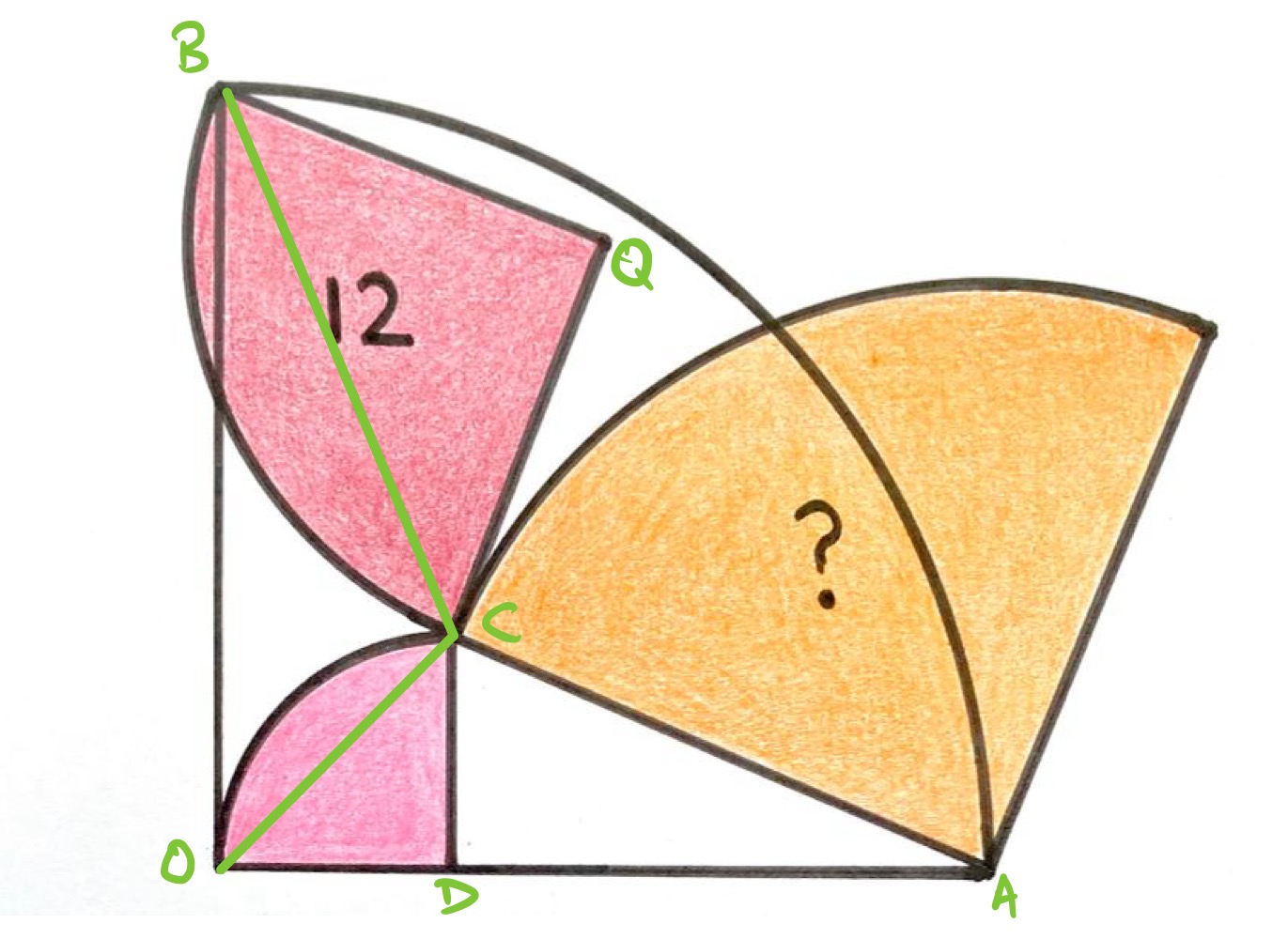
Consider the diagram labelled as above. Triangle is an isosceles right-angled triangle as it comes from the quarter circle, therefore angle is . Angle is then , so then triangles and are such that they have the same angle at with adjacent sides of equal length. Therefore they are congruent.
This means that line segments and have the same length. As triangle is also an isosceles right-angled triangle, has length times that of . Therefore, the yellow quarter-circle is times larger than the red quarter-circle. Its area scales by .
Hence the area of the yellow quarter-circle is .
Created on November 14, 2025 22:09:01 by Andrew Stacey (81.109.65.126).
These are the techniques used in solving the problem four squares ix.
Created on November 14, 2025 22:07:48 by Andrew Stacey (81.109.65.126).
Four Squares. What’s the angle?
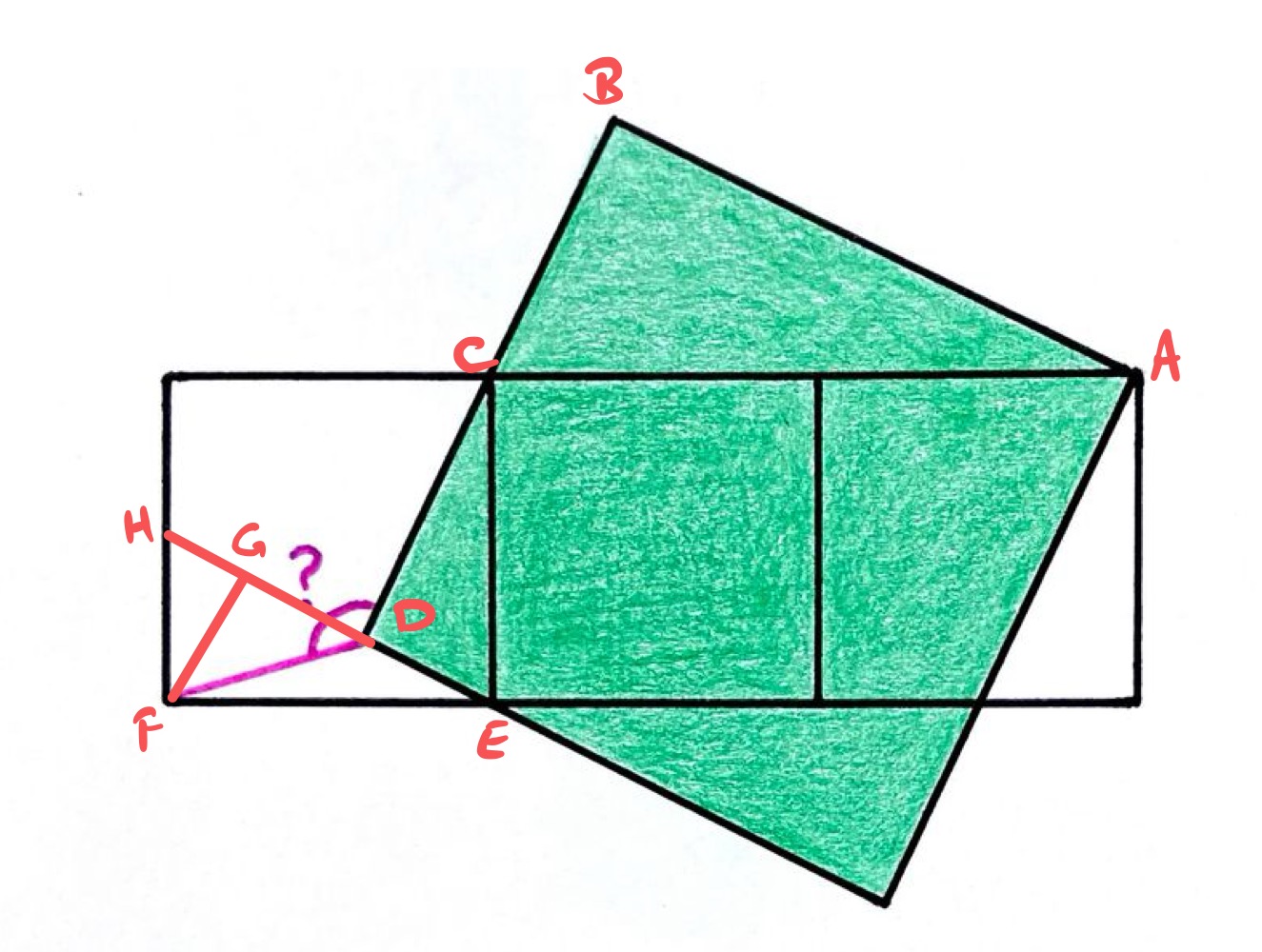
In the above diagram, line segment is the continuation of , and is such that angle is .
Angles , , and add up to since they are angles at a point on a straight line, therefore angles and add up to , since angle is . Then also angles and add up to since is a right-angled triangle. Hence angles and are the same, so triangles and are similar.
Since line segment has twice the length as , so also has twice the length of . But then since has the same length as , this means that also has twice the length of .
Angles and add up to , so triangles and are likewise similar, but then as line segments and are sides of the same square, they have the same length. So in fact, triangles and are congruent.
This means that line segment has twice the length of both line segments and . Therefore, line segments and have the same length, so triangle is an isosceles right-angled triangle.
Therefore, angle is , so angle is .
Created on November 11, 2025 23:07:09 by Andrew Stacey (81.109.65.126).
Posted on July 5, 2025

The three rectangles are congruent. What fraction of the design is shaded?
Created on November 11, 2025 23:05:31 by Andrew Stacey (81.109.65.126).
Posted on June 28, 2025

Four quarter circles. What’s the area of the orange one?
Created on November 11, 2025 23:03:30 by Andrew Stacey (81.109.65.126).
Posted on June 14, 2025

Four squares. What’s the blue square’s area?
Created on November 11, 2025 23:02:44 by Andrew Stacey (81.109.65.126).
Posted on June 21, 2025

These triangles are congruent and isosceles. What’s the area of the semicircle?